题目描述

给定一颗树，树中包含 n个结点（编号 1∼n）和 n−1条无向边。

请你找到树的重心，并输出将重心删除后，剩余各个连通块中点数的最大值。

重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

输入格式
第一行包含整数 n，表示树的结点数。
接下来 n−1行，每行包含两个整数 a和 b，表示点 a和点 b之间存在一条边。

输出格式
输出一个整数 m，表示将重心删除后，剩余各个连通块中点数的最大值。

数据范围
1≤n≤105

样例

输入样例
9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6
输出样例：
4

DFS

树与图的深度优先遍历（采用邻接表）

基本思想：

原理图：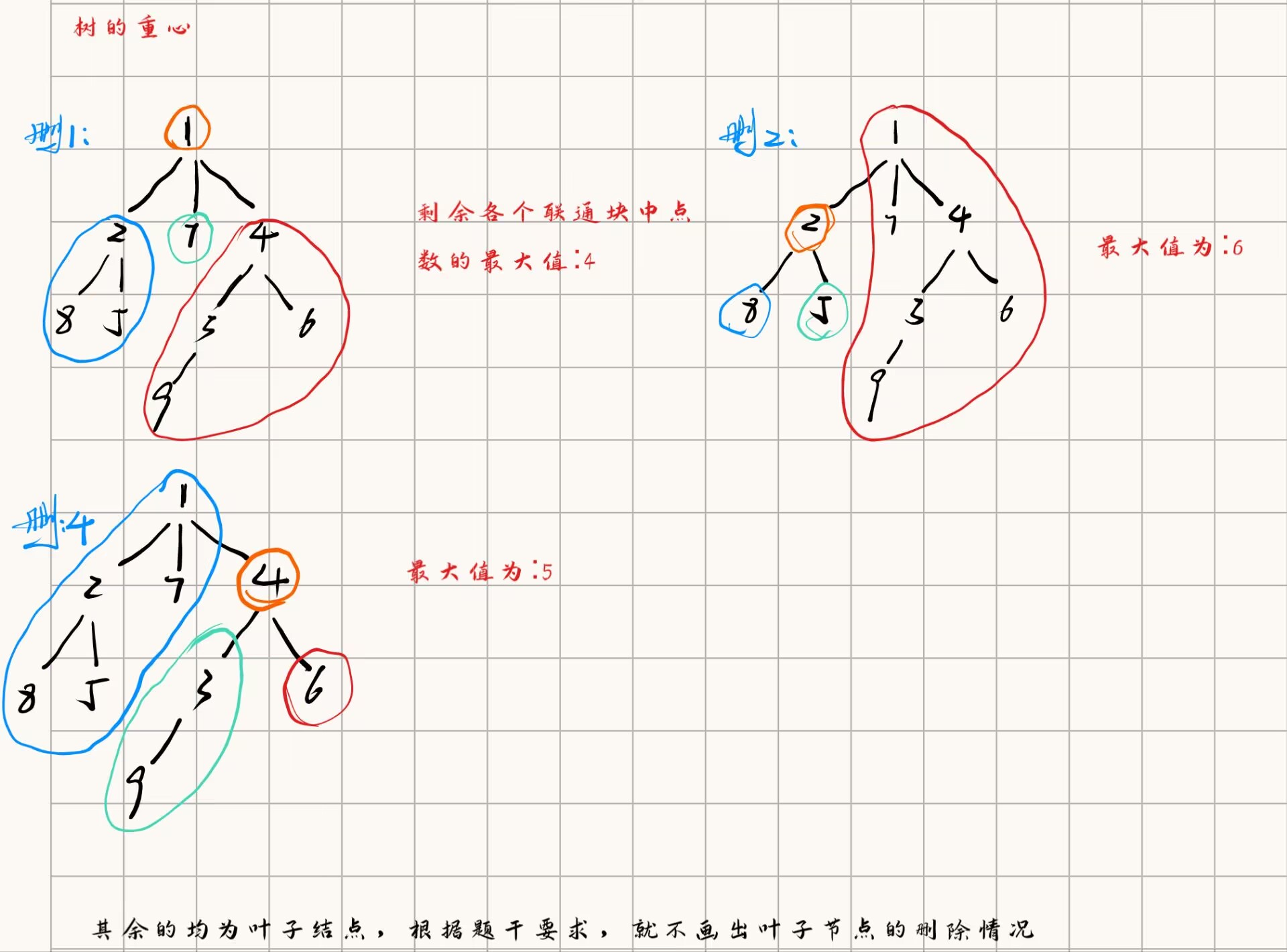

讨论：
1.为何在dfs函数中返回sum，而不是ans？
首先我们需要明确数组res，ans和sum分别代表什么
res：res 变量在 dfs 函数中用于存储子树中最大的独立集的大小,即连通块中点数的最大值
ans：ans 变量用于记录全局最小的独立集大小，即各个连通块中点数的最大值中的最小值
sum：sum 变量在 dfs 函数中用于累计当前节点的子树大小，包括当前节点本身

  由于在dfs函数的实现部分中，代码的执行顺序为：res = max(res, n - sum);  ans = min(ans, res); 
  说明res和ans都直接或者间接与sum相关，即：先求出sum，才能求出res，然后才能求出ans
  所以dfs函数返回sum值的大小便于找到删除每一个点后其最小的“最大连通块”的大小，即树的重心

2.为什么是add(a,b),add(b,a);?
由题干信息可知，“每行包含两个整数 a和 b，表示点 a和点 b之间存在一条边”，说明该图是无向图
对于无向图而言，每条边都是双向的，所以调用两次add函数去构造双向的边

3.为什么dfs函数可以选择任意的数字？
因为在树这种数据结构中，由于其没有环的特性，dfs函数可以从任意节点开始遍历，最终都能访问到所有其他节点。选择从节点1开始dfs只是一个起点，因为树是连通的，从任意节点开始dfs都能遍历整棵树。

4.为什么是res = max(res, n - sum) 而不是 res = max(res, n - res)?
1.sum 的含义：sum 表示当前节点 u 的子树中所有节点的数量。当我们考虑删除以 u 为根的子树时，sum 就是被删除的节点数量。

  **n - sum 的含义**：n - sum 表示在删除以 u 为根的子树后，树中剩余的节点数量。这些剩余的节点将形成一个或多个连通块。n - sum 实际上是在考虑如果当前子树被完全删除，剩下的树的大小，这可能是一个连通块，
  也可能因为删除子树而分成多个连通块。

  **为什么不是 n - res：**
  res 表示当前子树中最大的独立集的大小，即当前子树中不与子树中其他节点相连的节点集合的最大可能大小。如果我们使用 n -res，那么我们实际上是在考虑整个树中除了最大的独立集之外的节点数量，这与我们要计算的删除当前子树后剩余部分的最大连通块的大小无关。

res = max(res, n - sum) 这行代码的逻辑是：对于当前节点 u 的子树，我们考虑两种情况：

情况一：当前子树中最大的独立集的大小（res）。
情况二：如果我们删除整个子树，剩余的树的大小（n - sum），这将是剩余部分的最大连通块的大小。

下面是代码实现：

C++ 代码

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 100010, M = N * 2;

int n;

// e 数组是用来存储图中每个边指向的节点的索引，而 idx 是用来记录当前添加的边在 e 和 ne 数组中的位置
// 数组 ne[i] 表示的是图的邻接表中第 i 条边的下一条边的索引。
// 具体来说，ne 数组用于构建一个链表，每个节点在 ne 数组中都指向它的下一条邻接边在 e 数组中的位置。
// 数组h[N]表示的是邻接表

int h[N], e[M], ne[M], idx;

// 定义布尔数组st，用于标记节点是否被访问过
bool st[N];

int ans = N;

int dfs(int u)
{
  st[u] = true;  

  int sum = 1, res = 0;

  for(int i = h[u]; i != -1; i = ne[i])
  {
    int j = e[i];

    if(!st[j]) 
    {
      int s = dfs(j);
      res = max(res, s);
      sum += s;
    }
  }
  res = max(res, n - sum);

  ans = min(ans, res);


// 关于为什么会return sum， 我们知道ans存储的是找到的最小的“最大连通块”的大小，而sum存储的是当前节点及其所有子节点的总数
// 这就意味着当我们每次遍历树/图中每一个点去得到ans之前，都必须先找到sum值的大小，因为 res = max(res, n - sum), ans = min(ans,res)
// 所以dfs函数返回sum值的大小以便于找到删除每一个点后其最小的“最大连通块”的大小，即树的重心


  return sum;
}


void add(int a, int b)
{
  e[idx] = b, ne[idx] = h[a], h[a] = idx ++; 
}

int main()
{
  cin >> n;

  memset(h, -1, sizeof h);

  for(int i = 0; i < n; i ++)
  {
    int a, b;
    cin >> a >> b;


    //题干中给出的条件为两点之间存在一条边，说明该树是无向图，对于一个无向图来说，每一条边都是双向的

    add(a,b), add(b,a);
  }

  dfs(1);


  //输出最小的“最大连通块”的点的数量

  cout << ans << endl;

  return 0;
}