数字三角形

传送门

经典的线性dp问题，也不难
基于y氏的dp法分析过程

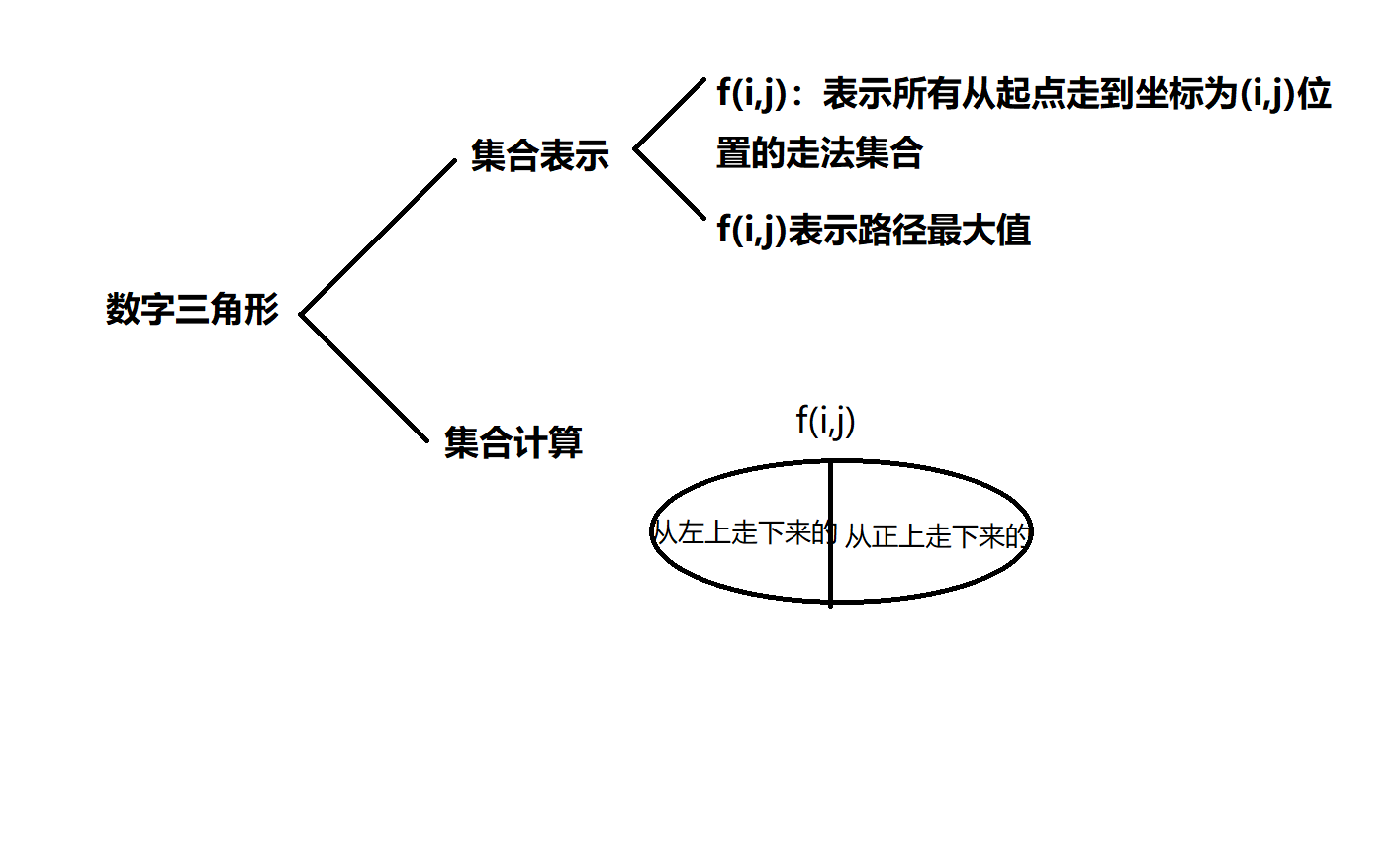
在计算时，我们只需要
取从正上和左上走下来的路径最大值，再加上当前路径的值，就是我们当前点所有路径的最大值

具体细节见代码注释

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;
const int N = 510;
int m[N][N],f[N][N];
int n;
const int INF=10e7;//因为是求最大值，所以先将路径值设为负无穷大

int main()
{
    cin>>n;
    //初始化的时候需要多初始化一点
    //防止边界点计算过程中的越界问题
    for(int i=0;i<=n;i++)
    {
        for(int j=0;j<=i+1;j++)
        {
            f[i][j]=-INF;
        }
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=i;j++) scanf("%d", &m[i][j]);
    }
    f[1][1]=m[1][1];
    for(int i=2;i<=n;i++)
    {
        for(int j=1;j<=i;j++)
        {
        //状态转移
            f[i][j]=m[i][j]+max(f[i-1][j],f[i-1][j-1]);
        }
    }
    int res=-INF;
    //最后是求所有到达最后一层的路径最大值
    for(int i=0;i<=n;i++) res=max(res,f[n][i]);

    cout<<res<<endl;



    return 0;
}