最长公共子序列

传送门

本题的y氏dp分析图

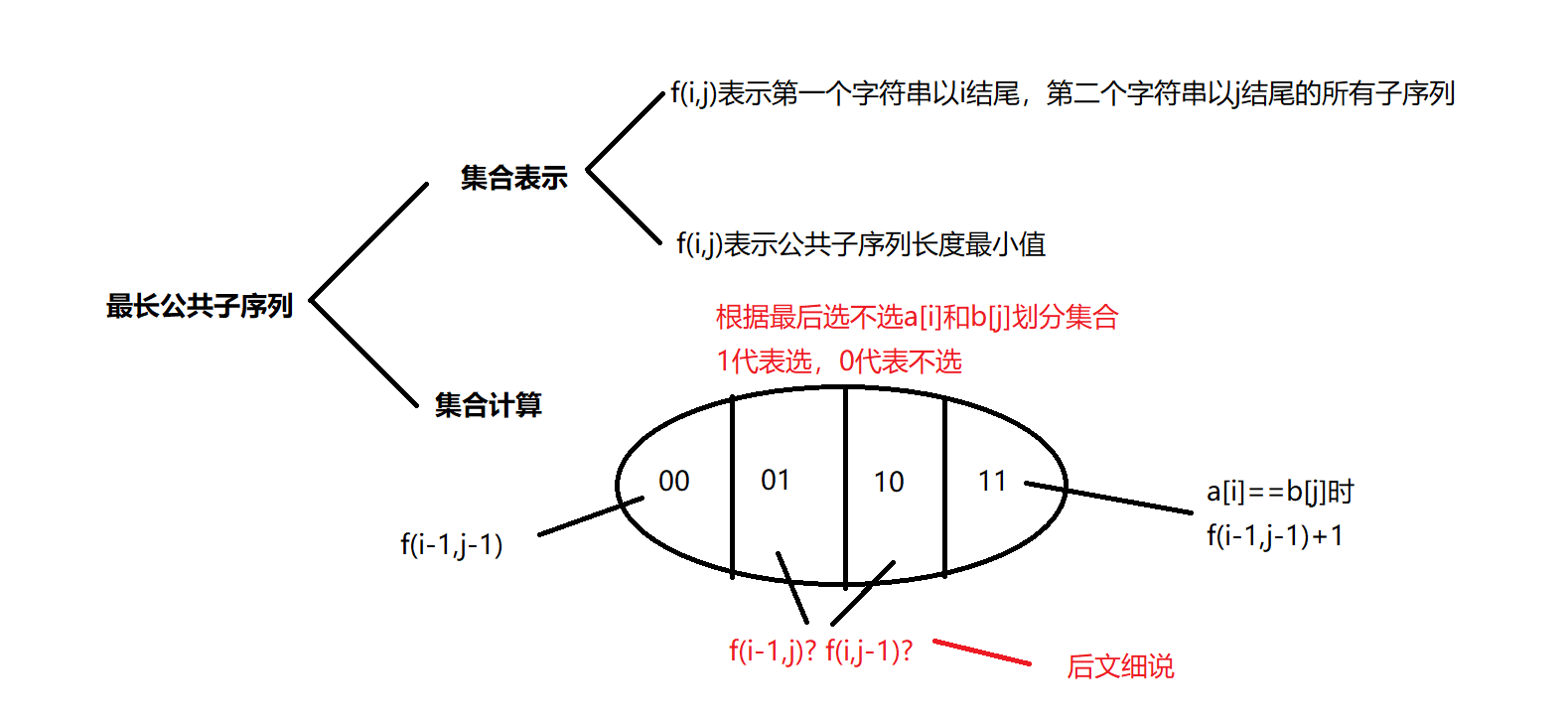
本题我们需要注意的问题就是中间两个集合到底怎么算，能不能像图中这样简单的表示？

答案是否定的

就以f(i-1,j)举例子，我们本来是想用它来表示不选a[i]而选b[j]的状态
但我们定义的状态f表示的是i-1和j的所有子列，子列中，我们不一定会选上b[j]，但是我们在计算中又要必须选上b[j]。所以它们是不等价的

不过还好，f(i-1,j)这个状态能包含我们的要求(包含选b[j]的情况，不过不含不选b[j]的情况)，f(i,j-1)也同理，所以，我们在想，有什么方法能让我们的要求用这两个状态表示出来呢？

注意到，它们两个集合之间的公共部分，就是同时不选a[i]和b[j]的情况，也就是f(i-1,j-1)

同样注意到，在求最大值之间，是允许有公共部分重叠的

例如求这两个集合的最大值{10,2},{2,1}，即使有公共部分，我们仍然能求出正确的最大值10

虽然有重叠部分，我们可以不关心，在状态转移中，直接用来求最大值是可行的

在实际计算中，f(i-1,j-1)被包含在f(i-1,j)和f(i,j-1)中，所以可以不用考虑

详细细节请参见代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 10010;
char a[N],b[N];
int f[N][N];
int n,m;

//f(i-1,j-1),f(i-1,j),f(i,j-1),f(i,j)
//00,        01,      10,      11

int main()
{
    scanf("%d%d", &n, &m);
    scanf("%s%s", a+1,b+1);

    for (int i = 1; i <= n; i ++ )
    {
        for (int j = 1; j <= m; j ++ )
        {
            f[i][j]=max(f[i-1][j],f[i][j-1]);
            if(a[i]==b[j])//相等的情况 f[i][j]=max(f[i][j],f[i-1][j-1]+1);
        }
    }
    cout<<f[n][m]<<endl;
    return 0;
}