区间dp问题，石子合并

所谓区间dp问题，就是在状态表示中，状态是一个区间的这一类问题

传送门

本题的y氏dp分析图如下

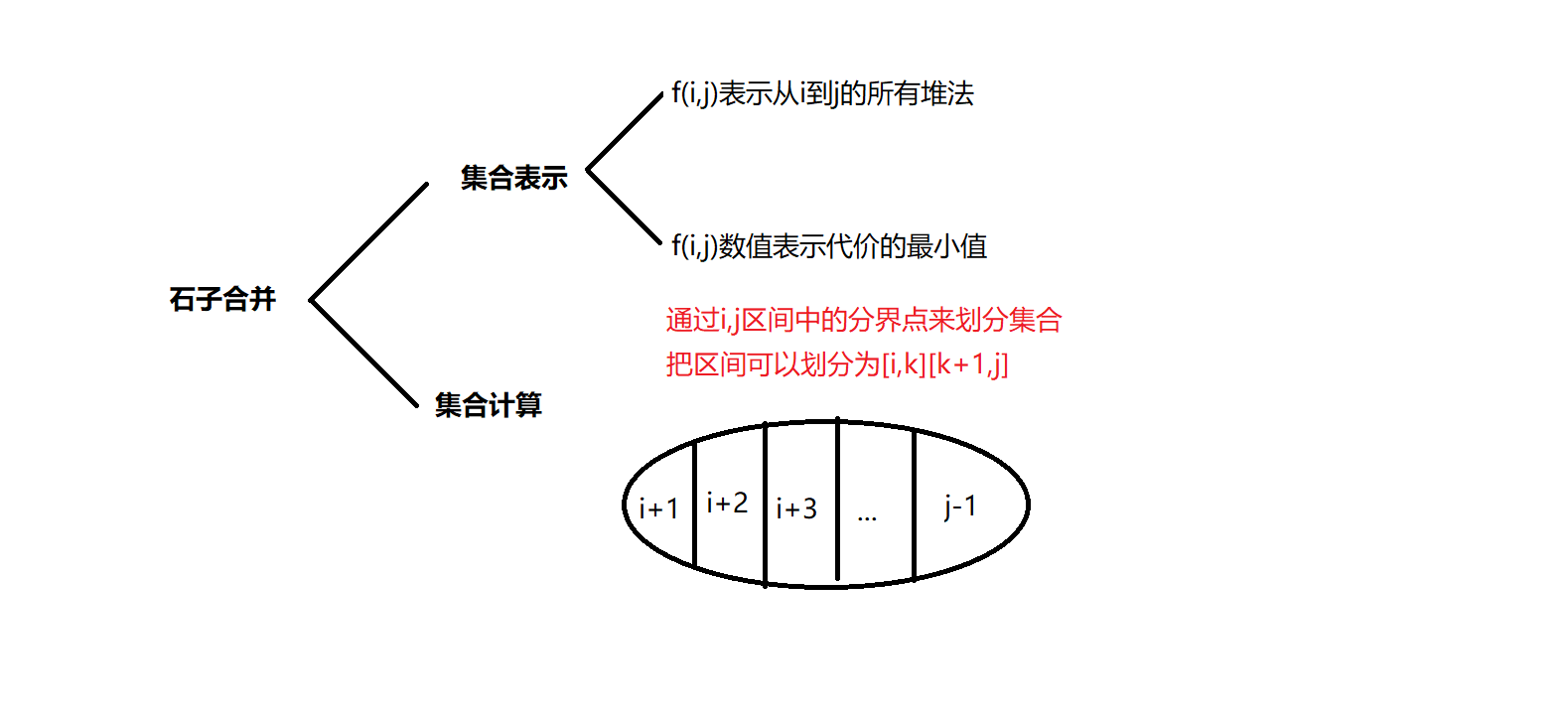
在状态转移计算中，我们只需要考虑最后一步的计算

即假设[i-k][k+1-j]已经分好了，我们最后把这两堆合并在一起的总代价

由于总代价需要求和，我们可能首先需要前缀和处理

具体细节请参见代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 310;
int n;
int a[N],f[N][N];
//从i到j的方法最小代价，划分通过区间内分界划分
int s[N];//因为代价是区间和，所以自然想到要用前缀和

int main()
{
    cin>>n;
    for (int i = 1; i <= n; i ++ )scanf("%d",&a[i]);
    //前缀和处理
    for (int i = 1; i <= n; i ++ ) s[i]=a[i]+s[i-1];

    //请注意，要先枚举区间长度，再枚举左端点

    for(int len=2;len<=n;len++)
    {
        for(int i=1;i+len-1<=n;i++)
        {
            int l=i;
            int r=i+len-1;//通过长度计算右端点
            f[l][r]=10e7;
            for(int k=l;k<r;k++)//枚举分界点，也就是在哪儿分开合并区间
            {
                //这里考虑的是区间内合并的最后一步
               //状态转移：左区间的代价加右区间的代价
              //再把它们两个大堆最后合并起来的代价 f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);
            }

        }
    }
    cout<<f[1][n]<<endl;//最后整个大区间的最小值就是我们的答案


    return 0;
}