题目描述

给定一个按照升序排列的长度为 n
的整数数组，以及 q
个查询。

对于每个查询，返回一个元素 k
的起始位置和终止位置（位置从 0
开始计数）。

如果数组中不存在该元素，则返回 -1 -1。

输入格式
第一行包含整数 n
和 q
，表示数组长度和询问个数。

第二行包含 n
个整数（均在 1∼10000
范围内），表示完整数组。

接下来 q
行，每行包含一个整数 k
，表示一个询问元素。

输出格式
共 q
行，每行包含两个整数，表示所求元素的起始位置和终止位置。

如果数组中不存在该元素，则返回 -1 -1。

数据范围
1≤n≤100000

1≤q≤10000

1≤k≤10000

样例

输入样例：
6 3
1 2 2 3 3 4
3
4
5
输出样例：
3 4
5 5
-1 -1

根据灵茶山艾府的思路总结得出的步骤

1. 确定查找区间：根据查找区间可以分出4种写法

• 左开右闭 L=-1 ，R=n-1
• 闭区间 L=0，R=n-1
• 左闭右开 L=0，R=n
• 开区间 L=-1，R=n

2. 对于判断结束循环的条件：本质保持区间不为空 ,如闭区间上 l <= r ,其他可由闭区间改写

因区间改变而对 L 和 R 改变
* 闭区间 l <= r
* 左闭右开 l < r
* 左开右闭 l+1 <= r
* 开区间 l+1 < r

3. 选择中间数字：奇数取中间 ，偶数(L+R)/2向下取整或(l+r)>>1

4. 更新区间 : 保持更新后区间与原区间不变

将mid的对应的值和target比较 a[mid]>=targe
循环不变量： 如闭区间L-1始终为红色，R+1始终为蓝色
中间i为mid的值

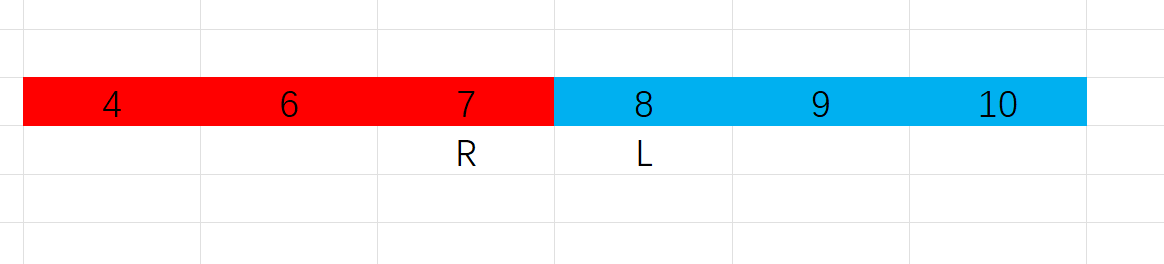
* 闭区间：

    nums[left-1] < target
    nums[right+1] >= target

• 左闭右开：

    nums[left-1] < target
    nums[right] >= target

• 闭区间

   L = mid+1  --->[ mid +1, right ]   
   R = mid -1 ---->[left  , mid-1 ]

• 左闭右开

  L = mid+1 --->[ mid +1, right )  
   R = mid ---->[left , mid )

• 开区间

   L = mid ---->(mid,right)
   R = mid ---->(left,mid)

5. 返回值

    1. 返回值 >x   可以看作 >=x+1
    < x    可以看作 >=x-1
    <=   可以看作  >x-1
    2.  二分: 返回最小的满足``numsi >= target``的 ``i``
    返回值由循环不变量决定,指向蓝色区域
    * 左闭右开&&左开右闭
    返回 left 还是 right 都行，因为循环结束后 left == right
    * 闭区间
    return l ；蓝色区循环不变量R+1=L , return l
    * 开区间
    return r ; 蓝色区域不变量为r
    * 如果``r == nums.size()||numsr！=target``   没有要查找的数字，返回数组长度

//开区间写法
#include<iostream>
#include<cstdio>
using namespace std;
const int N=1000010;
int n,q;
int a[N];
//二分查找
int lower_bound(int a[],int x)
{
    int l=-1,r=n;
    while(l+1<r)
    {
        int mid=(l+r)>>1;
        if(a[mid]>=x) r=mid;
        else l=mid;
    }
    return r;
}
int main()
{
    scanf("%d%d",&n,&q);
    for(int i=0;i<n;i++)
    {
        scanf("%d",&a[i]);
    }
    while(q--)
    {
        int x;
        scanf("%d",&x);
        int start=lower_bound(a,x);
        if(start==n||a[start]!=x) 
            cout<<"-1 -1"<<endl;
        else {
        int end=lower_bound(a,x+1)-1;
        cout<<start<<' '<<end<<endl;
        }
    }
    return 0;

}