本题可以翻译为给定一个无向图，求出删除某个点后，这个图剩下的部分至少要加几条边才可以把剩下的部分连通起来。


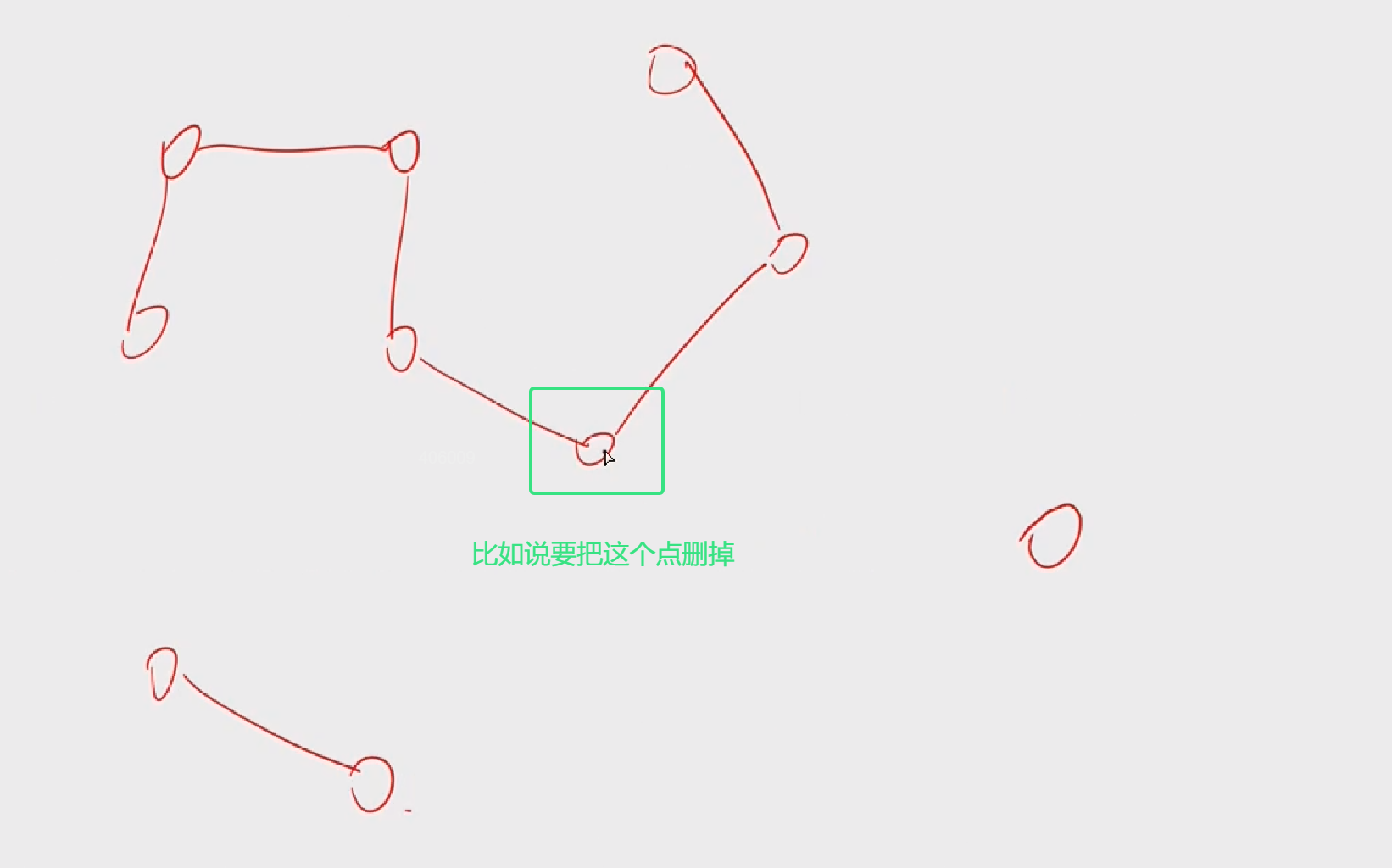
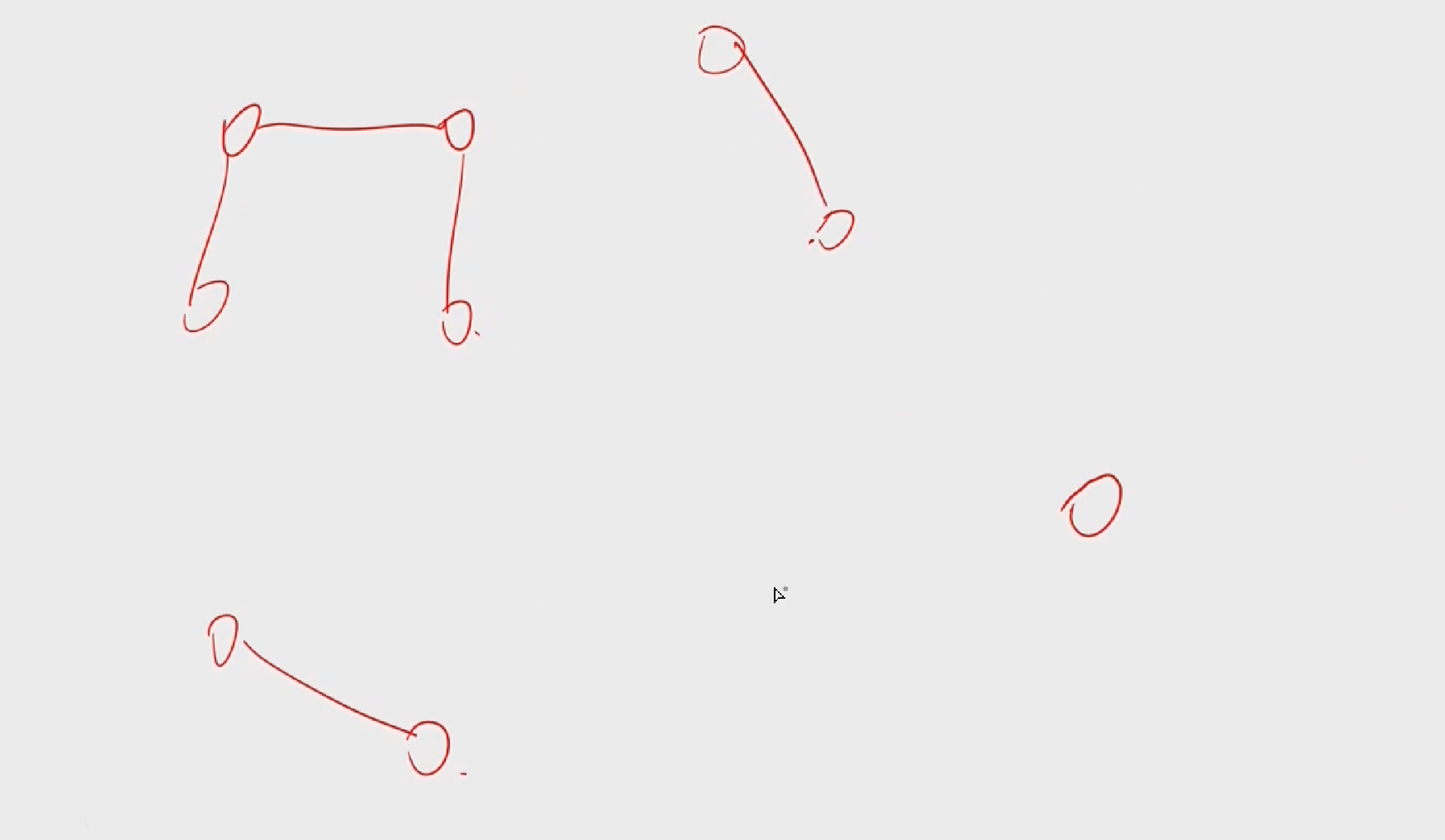
若想把剩余部分连通，最少要加几条边呢？我们可以发现剩余部分有4个连通块，每加一条边，最多可以把两个连通块合并，所以我们如果想把4个连通块合并成一个连通块的话，最少需要加3条边：

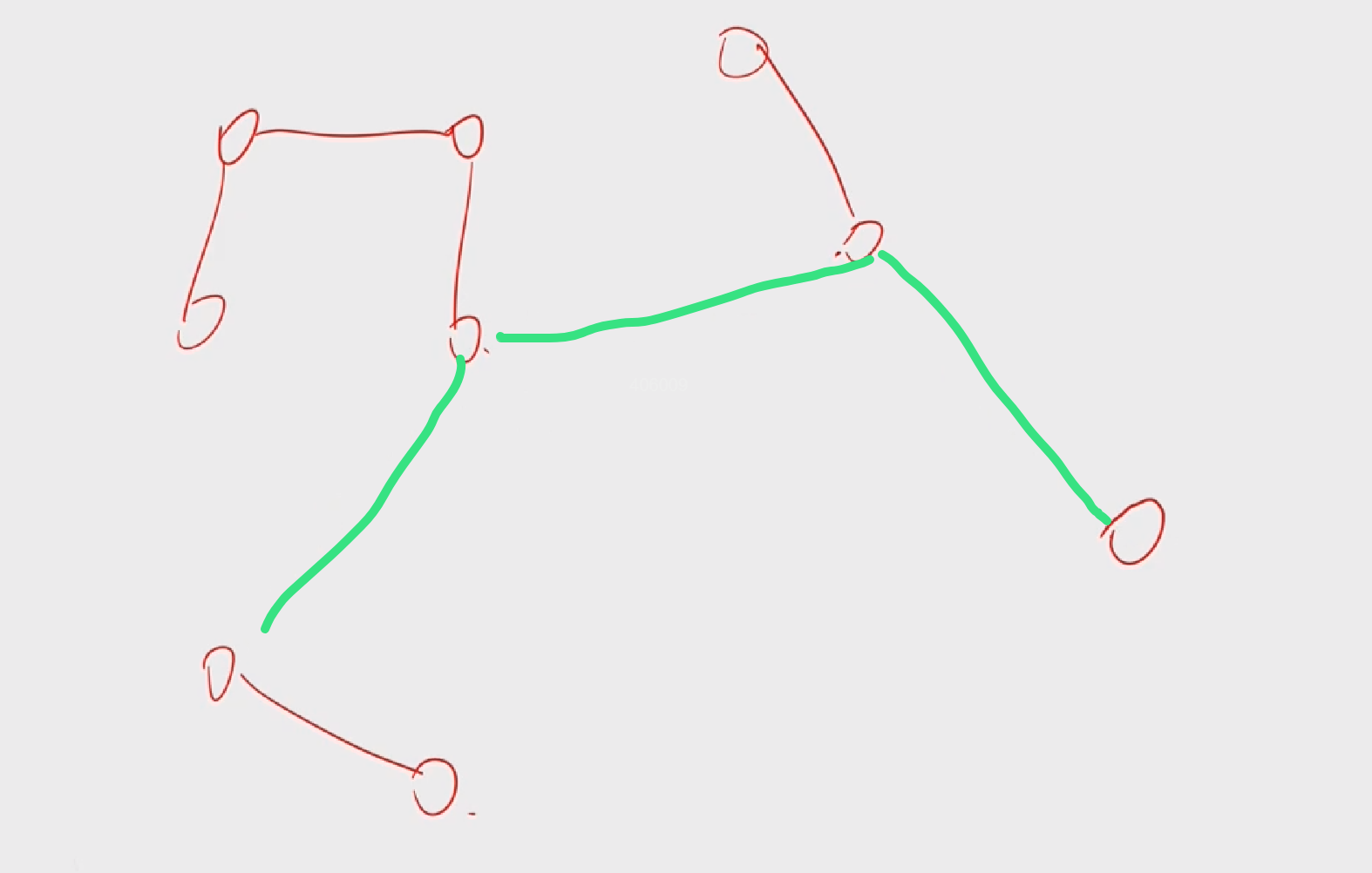
所以本题就可以转换为删掉某个点后，剩余部分可以构成多少连通块，求连通块的数量，ans = 连通块的数量 - 1

edges = []
p = [0] * 1010

def find(x):
    if x != p[x]:
        p[x] = find(p[x])
    return p[x]

n,m,k = map(int,input().split())

for i in range(m):
    edges.append(list(map(int,input().split())))

for x in map(int,input().split()):
    for i in range(1,n + 1): # 并查集初始化
        p[i] = i

    cnt = n - 1 # 连通块数量，初始时每个点都是一个连通块，去除x这个点，所以为n - 1

    for a,b in edges:# 枚举所有边
        if a != x and b != x: # 如果这条边不包含x顶点
            pa = find(a);pb = find(b)
            if pa != pb: # 若这两个连通块不连通
                p[pa] = pb # 合并这两个连通块
                cnt -= 1 # 连通块数量--

    print(cnt - 1)

超时了一个测试点，可以转C++代码