将整个串添加元素(最小代价)变为回文串, 等价于在原串中删除单一
(无回文字符匹配的)元素，即
从当前样子变成初始状态需要添加叶子的数量 等价于 当前样子变成最大的回文串需要剪去的叶子的数量
即至少脱落多少个种子 等价于 原串总长度 - 最大回文子序列的长度

做法1 : 将序列倒过来进行匹配最长公共子序列，在用初始长度减去

最长公共子序列的长度即为答案

import java.util.*;

public class Main {

    static final int N = 1010;
    static int[][] f = new int[N][N];

    public static void main(String[] args) {

        Scanner sc = new Scanner(System.in);

        char[] ch = sc.nextLine().toCharArray();
        int len = ch.length;
        char[] ch1 = new char[ch.length + 1], ch2 = new char[ch1.length + 1];
        for (int i = 1, j = len - 1; i < len; i ++, j--) {
            ch1[i] = ch[i - 1];
            ch2[i] = ch[j];
        }

        for (int i = 1; i <= len; i ++) {
            for (int j = 1; j <= len; j++) {
                f[i][j] = Math.max(f[i - 1][j], f[i][j - 1]);
                if (ch1[i] == ch2[j]) f[i][j] = Math.max(f[i][j], f[i - 1][j - 1] + 1);
            }
        }

        System.out.println(len - f[len][len]);
    }
}

区间dp解法

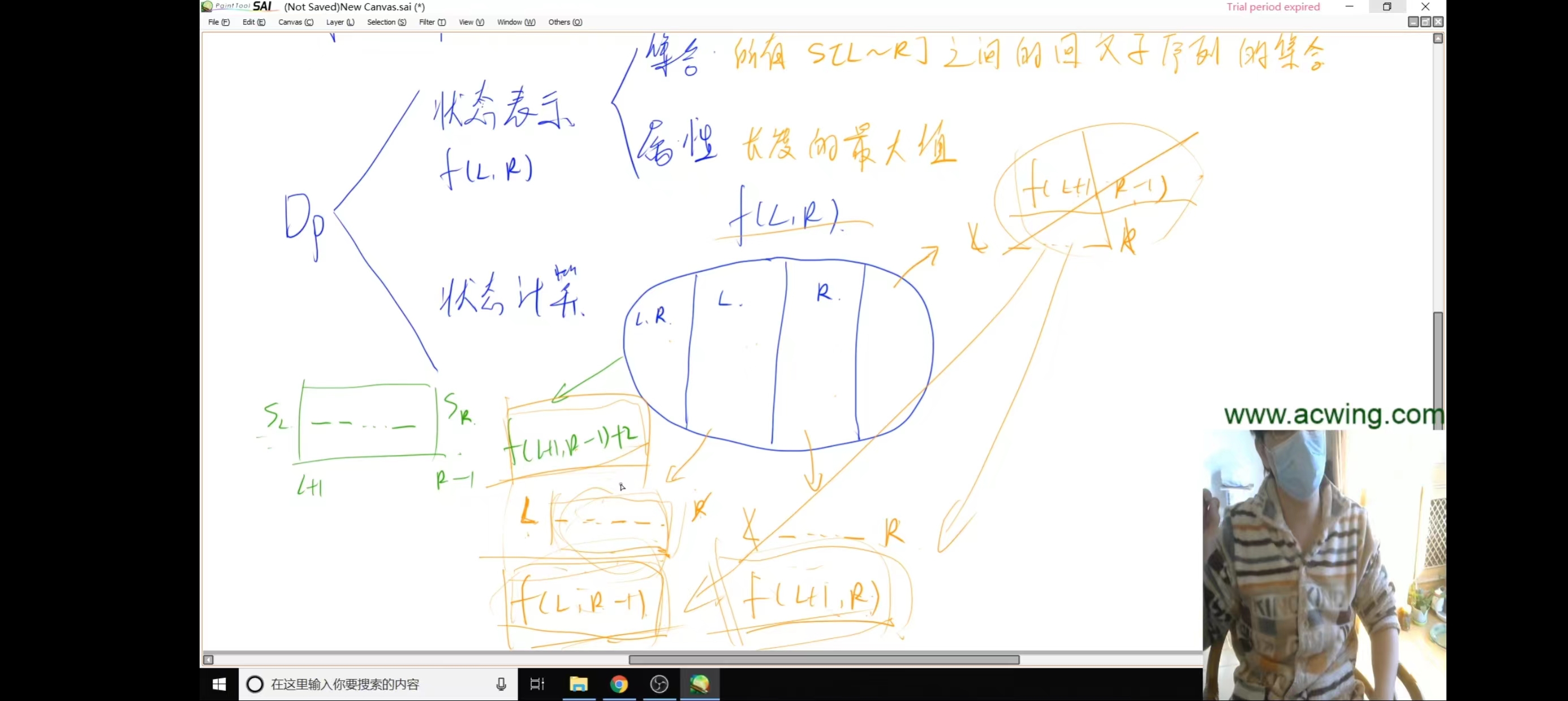
f[i][j] : 对字符数组ch，从ch[i] 到ch[j]的最长回文子序列的长度

import java.util.*;

public class Main {
    static final int N = 1010;
    static char[] ch = new char[N];
    static int[][] f = new int[N][N];

    public static void main(String[] args) {

        Scanner sc = new Scanner(System.in);

        ch = sc.nextLine().toCharArray();
        int n = ch.length;

        for (int len = 1; len <= n; len++) {//枚举长度
            for (int l = 0; l + len - 1 < n; l++) {//左右端点
                int r = l + len - 1;
                if (len == 1) f[l][r] = 1;//只有自己时
                else {
                    f[l][r] = Math.max(f[l + 1][r], f[l][r - 1]);//后三种情况最大值
                    //第一种情况去最值
                    if (ch[l] == ch[r]) f[l][r] = Math.max(f[l][r], f[l + 1][r - 1] + 2);
                }
            }
        }
        //ch的下标从0开始的
        System.out.println(n - f[0][n - 1]);
    }
}