树形dp

模型：找无向图中的连通块权值最大
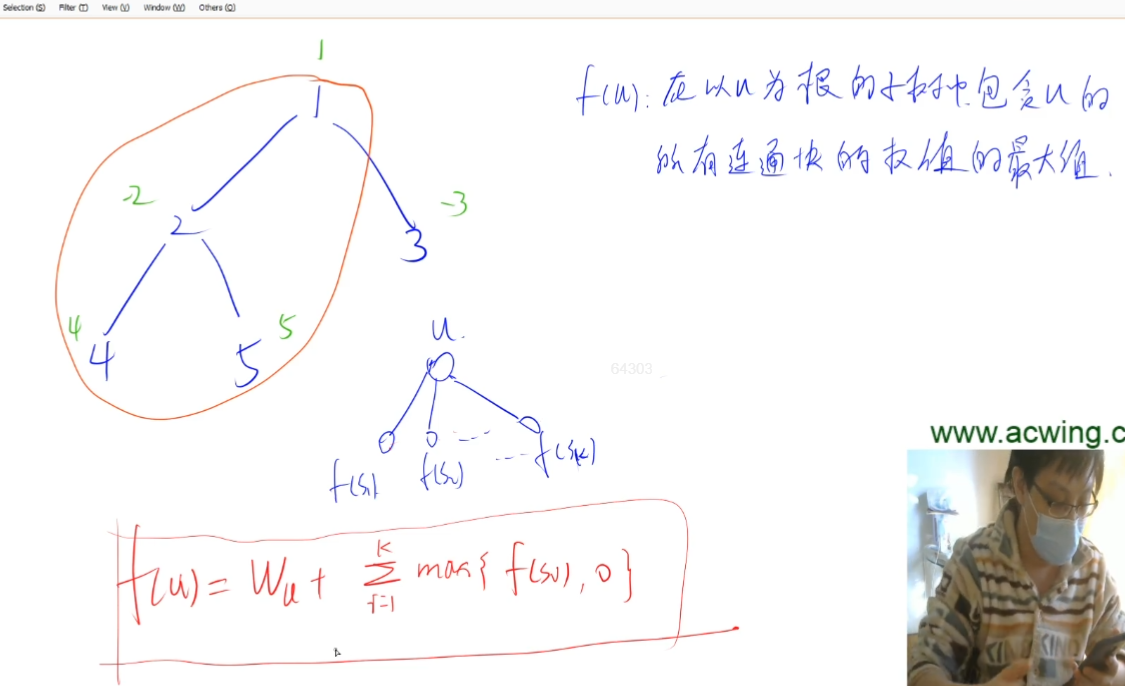
记f[i]表示以下标为i根节点的子树权值的最大值对于可能出现的f[j]负值问题，取零即可，
即不选以j为根节点的子树：f[i] = w[i] + (枚举i的所有子节点)Math.max(f[j], 0);

import java.util.*;
import java.io.*;

public class Main {

    static final int N = 100010, M = 2 * N;//无向图边的数量为点的二倍
    static long[] f = new long[N];//可能会爆int
    static int[] h = new int[N], e = new int[M], ne = new int[M], w = new int[N];
    static int idx, n;

    public static void main(String[] args) throws IOException {
        BufferedReader sc = new BufferedReader(new InputStreamReader(System.in));

        n = Integer.parseInt(sc.readLine());
        String[] s = sc.readLine().split(" ");
        //下标从1开始
        for (int i = 1; i <= n; i++) w[i] = Integer.parseInt(s[i - 1]);
        Arrays.fill(h, -1);//初始化

        for (int i = 1; i < n; i++) {
            String[] s2 = sc.readLine().split(" ");
            int a = Integer.parseInt(s2[0]), b = Integer.parseInt(s2[1]);
            add(a, b);
            add(b, a);
        }

        dfs(1, -1);

        long max = f[1];
        for (int i = 1; i <= n; i++) 
            if (max < f[i]) max = f[i];
        System.out.println(max);
    }

    /**
    * u : 枚举f[i]中的i
    * father : 记录从谁过来的(父节点)，无向图防止自循环
    */
    static void dfs(int u, int father) {
        f[u] = w[u];
        for (int i = h[u]; i != -1; i = ne[i]) {//枚举u的子节点
            int j = e[i];
            if (j != father) {
                dfs(j, u);//求解f[j]，传入j的父节点u
                f[u] += Math.max(0, f[j]);
            }
        }
    }

    static void add(int a, int b) {
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx++;
    }
}