树状数组

本质上是求前缀和，可以高效的求解动态前缀和log(n)的时间

树状数组另一道题目: 楼兰图腾 https://www.acwing.com/activity/content/code/content/9010675/

import java.util.*;
import java.io.*;

public class Main {
    static final int N = 100010;
    static int[] tr = new int[N];
    static int n, m;

    public static void main(String[] args) throws IOException {

        BufferedReader sc = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter out = new PrintWriter(System.out);

        String[] s2 = sc.readLine().split(" ");
        n = Integer.parseInt(s2[0]);
        m = Integer.parseInt(s2[1]);

        String[] s = sc.readLine().split(" ");
        for (int i = 1; i <= n; i++) {
            add(i, Integer.parseInt(s[i - 1]));
        }

        while (m -- > 0) {
            String[] s3 = sc.readLine().split(" ");
            int sel = Integer.parseInt(s3[0]);
            if (sel == 1) {
                add(Integer.parseInt(s3[1]), Integer.parseInt(s3[2]));
            } else {
                int ans = query(Integer.parseInt(s3[2])) - query(Integer.parseInt(s3[1]) - 1);
                out.println(ans);
            }
            out.flush();
        }
    }

    static void add(int idx, int x) {
        for (int i = idx; i <= n; i += lowbit(i)) tr[i] += x;
    }

    static int query(int r) {
        int res = 0;
        for (int i = r; i > 0; i -= lowbit(i)) res += tr[i];
        return res;
    }

    static int lowbit(int x) {
        return x & -x;
    }
}

线段树(类似堆的结构)

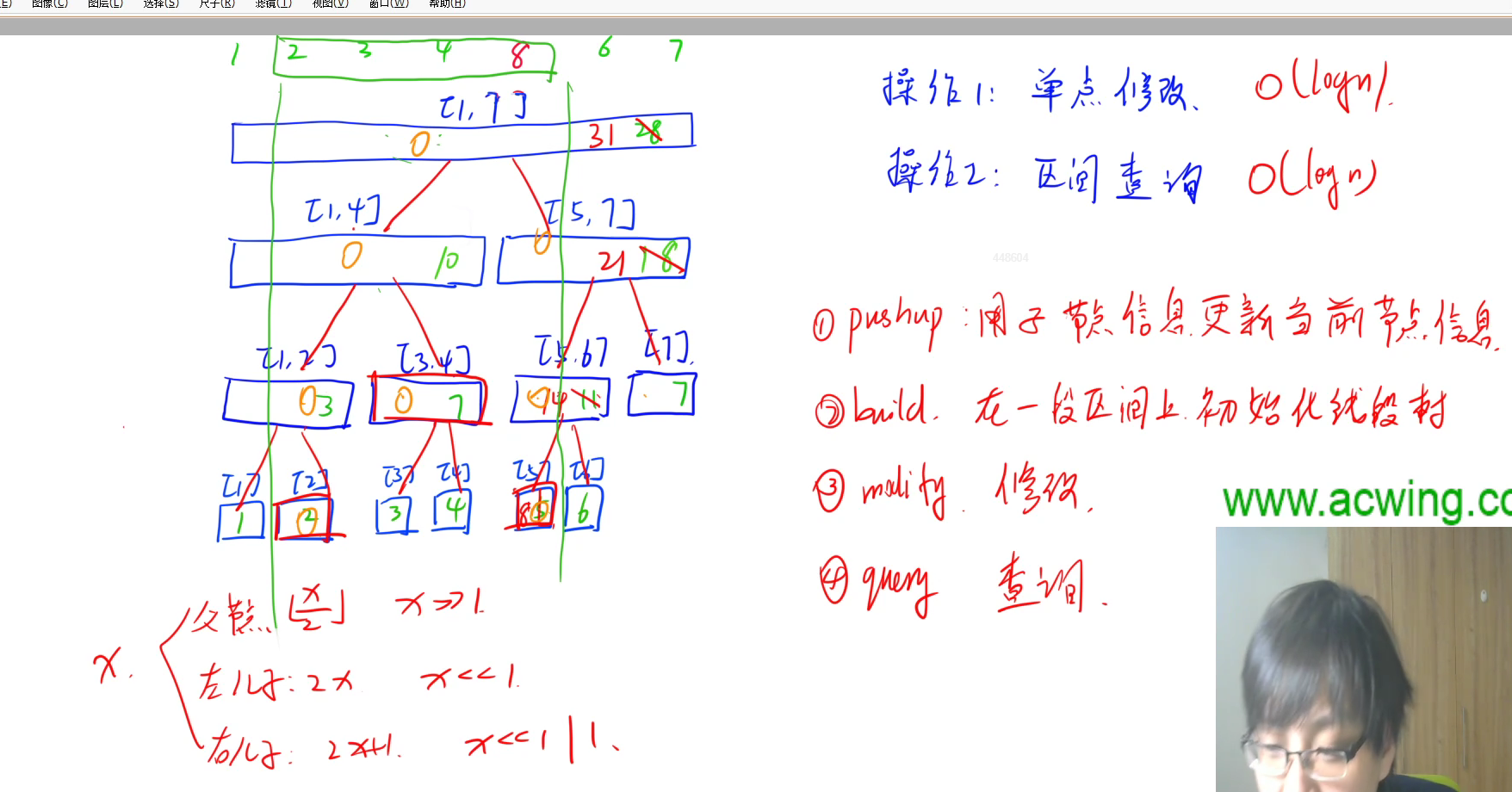
import java.io.*;

public class Main {
    static final int N = 100010;
    static int[] w = new int[N];//原数组

    static class Node {
        int l, r, sum;

        public Node(int l, int r, int sum) {
            this(l, r);
            this.sum = sum;
        }

        public Node(int l, int r) {
            this.l = l;
            this.r = r;
        }
    }

    static Node[] tr = new Node[4 * N];//最多不超过4n
    static int n, m;

    public static void main(String[] args) throws IOException {

        BufferedReader sc = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter out = new PrintWriter(System.out);

        String[] s2 = sc.readLine().split(" ");
        n = Integer.parseInt(s2[0]);
        m = Integer.parseInt(s2[1]);

        String[] s = sc.readLine().split(" ");
        for (int i = 1; i <= n; i++) {
            w[i] = Integer.parseInt(s[i - 1]);
        }

        build(1, 1, n);
        while (m-- > 0) {
            String[] s3 = sc.readLine().split(" ");
            int sel = Integer.parseInt(s3[0]);
            if (sel == 1) {
                modify(1, Integer.parseInt(s3[1]), Integer.parseInt(s3[2]));
            } else {
                out.println(query(1, Integer.parseInt(s3[1]), Integer.parseInt(s3[2])));
            }
            out.flush();
        }
    }

    /**
    * 通过u的儿子计算u的sum
    */
    static void pushup(int u) {
        tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
    }

    /**
    * 构建线段树
    * u : 根节点编号
    * l : 左边界
    * r : 右边界
    */
    static void build(int u, int l, int r) {
        if (l == r) tr[u] = new Node(l, r, w[r]);
        else {
            tr[u] = new Node(l, r);
            int mid = l + r >> 1;
            build(u << 1, l, mid);
            build(u << 1 | 1, mid + 1, r);
            pushup(u);
        }
    }

    /**
    * 查询l~r的前缀和
    * u : 父节点编号
    */
    static int query(int u, int l, int r) {
        if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
        int mid = tr[u].l + tr[u].r >> 1;
        int sum = 0;
        if (l <= mid) sum = query(u << 1, l, r);//如果左边有交集的话(个数为奇数的时候给左儿子多分配一个)
        if (r > mid) sum += query(u << 1 | 1, l, r);//右边有交集的话(也可以写成r >= mid + 1)
        return sum;
    }

    /**
    * 修改编号为x下的数值+c(=> add),如果是修改的话直接赋值即可
    * u
    * x : 修改节点的下标
    * c ：要变化的数值
    */
    static void modify(int u, int x, int c) {
        if (tr[u].l == tr[u].r) tr[u].sum += c;
        else {
            int mid = tr[u].l + tr[u].r >> 1;
            if (x <= mid) modify(u << 1, x, c);
            else modify(u << 1 | 1, x, c);
            pushup(u);
        }
    }
}