题目描述

你拿到了一棵树，请你给每个顶点染成红色或蓝色。
要求：每个红点周围有且仅有一个红点，每个蓝点周围有且仅有一个蓝点。
“周围”的定义：某点周围的点指通过邻边直接连接的点。
所谓树，即没有自环、重边和回路的无向连通图。

输入描述:

第一行一个正整数𝑛，代表树的顶点个数。(1≤𝑛≤100000)接下来的𝑛−1行，每行两个正整数
𝑢和𝑣，代表点 u 和点𝑣有一条边连接。(1≤u,v≤n) 保证输入的一定是一棵合法的树。

输出描述:

如果可以达成染色的要求，请输出一个长度为n 的字符串，第i 个字符代表第
i 个顶点的染色情况，’B’ 代表蓝色，’R’ 代表红色。
（若有多种合法染色的方法，输出任意一种即可）
否则直接输出-1。

分组过程

例子1(未匹配)

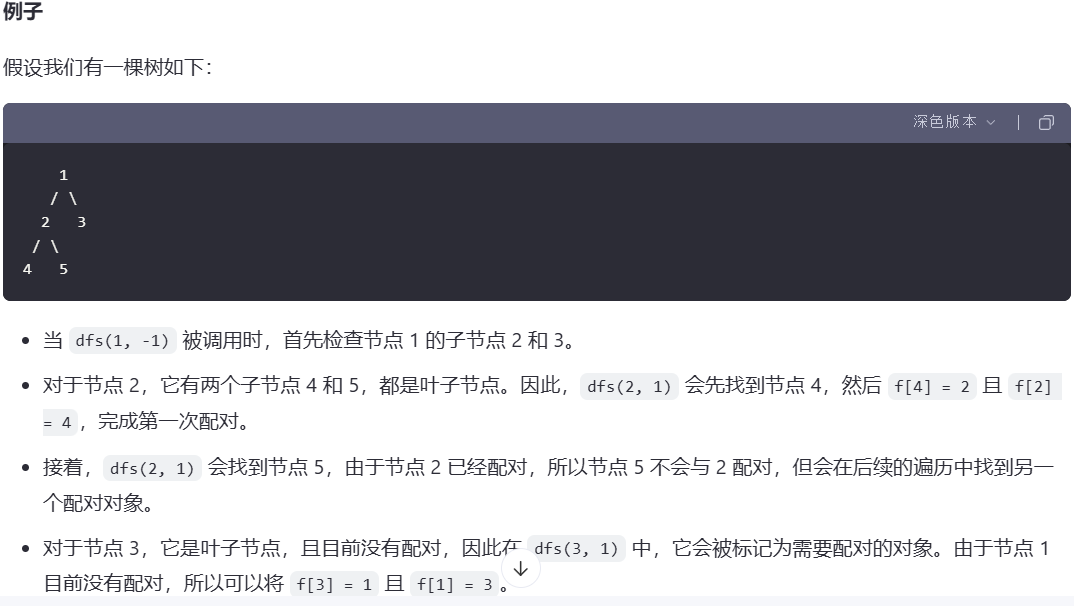
例子2(匹配)

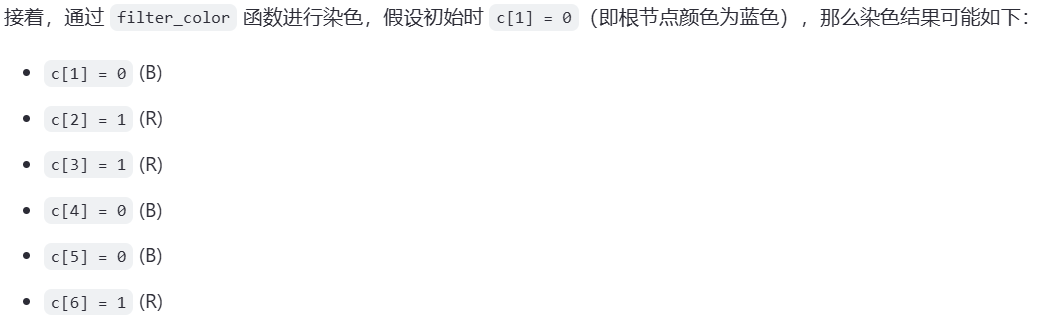
import java.util.*;
import java.io.*;

public class Main {
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    static PrintWriter out = new PrintWriter(System.out);
    static final int N = 100010;
    static int[] h = new int[N], e = new int[2 * N], ne = new int[2 * N];
    /**
     * g[i] 表示与节点 i 配对的节点编号。如果一个节点没有配对，则 g[i] 为 0。
     * 颜色数组 col[i] 表示节点 i 的颜色。
     */
    static int[] g = new int[N], col = new int[N];
    static int n, idx;

    public static void main(String[] args) throws IOException {
        n = Integer.parseInt(br.readLine());

        Arrays.fill(h, -1);

        for (int i = 1; i < n; i++) {
            String[] str = br.readLine().split(" ");
            int a = Integer.parseInt(str[0]), b = Integer.parseInt(str[1]);
            add(a, b);
            add(b, a);
        }

        dfs(1, -1);

        //遍历g数组如果有没有配对的点就代表无法进行染色   
        for (int i = 1; i <= n; i++) {
            if (g[i] == 0) {
                System.out.println(-1);
                return;
            }
        }

        fill_color(1, -1);
        for (int i = 1; i <= n; i++) {
            if (col[i] == 1) out.print('R');
            else out.print('B');
        }

        out.flush();
    }

    /**
     * 填充颜色
     * @param u 要进行染色的节点
     * @param fa u节点从哪里来(上一个节点)
     */
    static void fill_color(int u, int fa) {
        for (int i = h[u]; i != -1; i = ne[i]) {
            int j = e[i];
            if (j == fa) continue;//防止回路
            //如果节点 j 和节点 u 是一组，则它们的颜色相同；否则，它们的颜色相反。
            if (g[j] == u) col[j] = col[u];
            else col[j] = col[u] ^ 1;
            fill_color(j, u);//从根节点开始染色
        }
    }

    /**
     * dfs 方法用于遍历树，并对叶子节点进行配对。
     * @param u 要配对的节点
     * @param fa 上一个节点
     */
    static void dfs(int u, int fa) {
        for (int i = h[u]; i != -1; i = ne[i]) {
            int j = e[i];
            if (j == fa) continue;//防止回路
            dfs(j, u);//从叶子结点开始分组
            //如果当前节点 u 和其子节点 j 都没有配对节点，则将它们配对。
            if (g[j] == 0 && g[u] == 0) {
                g[j] = u;
                g[u] = j;
            }
        }
    }

    static void add(int a, int b) {
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx++;
    }
}