题目描述

求有限制边的最短路

• 一、为什么使用Bellman_ford?

  Bellman_ford作为求最短路的算法之一，主要通过n次的迭代来更新每一条边，时间复杂是O(nm),这里的n次是有实际意义的。例如此题限制走的边数为k，就可以通过k次迭代来更新每一条边，超过k次更新过的说明走过的边数一定大于k，则不符。

• 二、针对直播时提出的负权回路

  1.什么是负权回路？

  

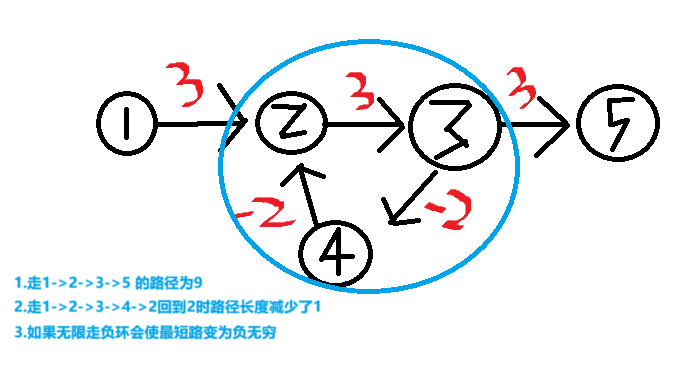
  2.怎么求

  bellman_ford也可以用来求负权回路，即当第n次迭代时有进行更新，说明走的边数大于n，则一定存在负权回路，但时间复杂度较高，可以用spfa求负权回路（添加一个经过边数的变量k，当k大于n说明步数大于n，则存在负环）。

  3.注意

  有负权回路也可能存在最短路，当通往终点的路线中部经过存在负权回路的那条，则存在最短路。

• 三、为什么要backup（记录前一次的dist[]）

  为了防止在某一次的迭代中用到本次循环中已经更新过的数据，造成串联。例如下图：
  
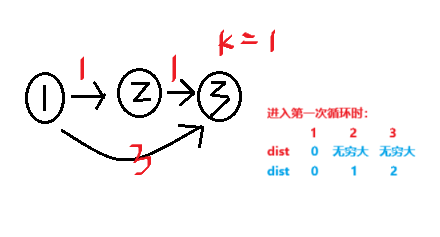
  这里dist[3]因为dist[2]的变化更新成了2，但是边数大于了k不符合，所以错误。正确的做法应该是当2->3这条路时dist[3]=dist[2]+1(无穷大+1)，最终还是无穷大，循环到1->3时再更新成最小值3。

下面是我的代码

#include<bits/stdc++.h>
using namespace std;
#define int long long 
const int N = 1e6+10;

int n,m,k,dist[N],backup[N];

struct stu{
    int u,v,weight;
}s[N];//存边，bellman_ford不需要链式前向星，只需要能遍历到每一个边即可 

int bellman_ford()
{
    memset(dist,0x3f,sizeof dist);
    dist[1]=0;
    for(int i = 0; i < k ;i++)//迭代k次可以让步数小于等于k' 
    {
        memcpy(backup,dist,sizeof dist);
        //存上一次循环的，防止串联 
        for(int j=1;j<=m;j++)
        {
            int a = s[j].u,b = s[j].v,c = s[j].weight;
            dist[b] = min(dist[b],backup[a]+c); //取最小 
        }
    }

    return dist[n];

}


signed main()
{
    cin >> n >> m>> k;
    for(int i=1;i<=m;i++)
    {
        int a,b,c;
        cin >> a >> b >> c;
        s[i] = {a,b,c};
    }

    int t = bellman_ford();
    if(t >= 0x3f3f3f3f / 2)
        //这里是因为出现负边时会变成0x3f3f3f3f-2,所以判断条件不是== 
         cout << "impossible" << endl;
    else cout << t << endl;
}