博弈论问题

1.不难发现，最后操作结束之后Alice 和 Bob 的值异或起来会等于所有值的异或值。（用A表示Alice的值，用B表示Bob的值）
2.最后观察最后异或出来的值（用sum表示），如果这个值的二进制位为1，则最后A与B的值，相对于的二进制位肯定不同，（如果相同二进制位应该为0），根据二进制的权重判断（越高位的二进制的权重越高），从sum的二进制位的最高位判断，如果位1则A与B的最后大小会由此位判断，否则看次高位。
3.确定对应的二进制位之后，分情况讨论

平局情况的证明
必要性：
如果Alice和Bob打成平局，意味着他们最终选择的数的异或和相等，即 a = b。因此，他们的异或结果 a ^ b = 0。
充分性：
如果所有数的异或和为零，那么可以将这些数分成两个集合，使得每个集合内的数的异或和相等。这样，无论Alice和Bob如何选择，他们选择的数的异或和都会相等，因此会形成平局。
游戏策略分析
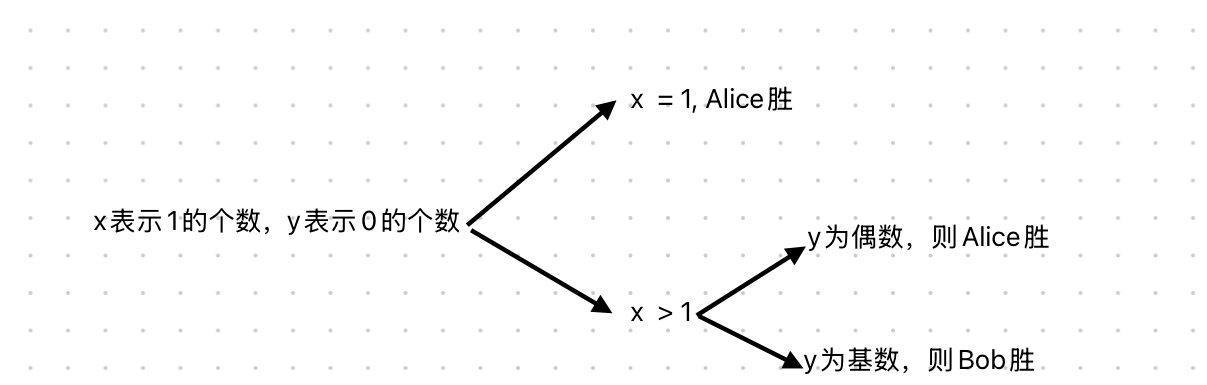
1. x = 1：
• 如果只有一个数的某一位是1，Alice可以先选择这个数，这样在这位上Alice就赢了，因为剩下的数在这位上都是0，不影响结果。
2. x 为偶数：
• 如果某一位上1的个数是偶数，那么这些1可以被分成两组，每组的个数相等，因此无论怎么选择，这一位上的结果总是平局。
3. x ≠ 1 且 x 为奇数：
• 如果某一位上1的个数是奇数，那么这些1不能被平均分成两组。这时，拿到奇数个1的人会赢。如果所有数的这一位都是1，那么先手会赢。但如果有0，那么后手可以通过选择0来改变先后手的顺序，从而获胜。
• 如果 n - x（即这一位上为0的数的个数）是偶数，那么先手仍然是先手，Alice会赢。如果 n - x 是奇数，那么后手会变成先手，Bob会赢。

#include <bits/stdc++.h>

using namespace std;

const int N = 20;

int main()
{
    int T;
    cin >> T;

    while (T -- )
    {
        int n;
        cin >> n;

        int cnt[N] = {0};
        int sum = 0;
        for (int i = 0; i < n; i ++ )
        {
            int t;
            scanf("%d", &t);
            sum ^= t;
            for (int i = N - 1; i >= 0; i -- )
            {
                if (t >> i & 1) cnt[i] ++ ;
            }
        }

        if (sum == 0)
        {
            printf("0\n");
        }
        else
        {
            int res;
            for (int i = N - 1; i >= 0; i -- )
            {
                if (sum >> i & 1)
                {
                    res = i;
                    break;
                }
            }

            if (cnt[res] == 1) puts("1");
            else
            {
                if ((n - cnt[res]) % 2 == 0) puts("1");
                else puts("-1");
            }
        }
    }

    return 0;

}