背包总结

注：本文为自我总结，会采用他人题解

01背包

题目 https://www.acwing.com/problem/content/2/

朴素版本

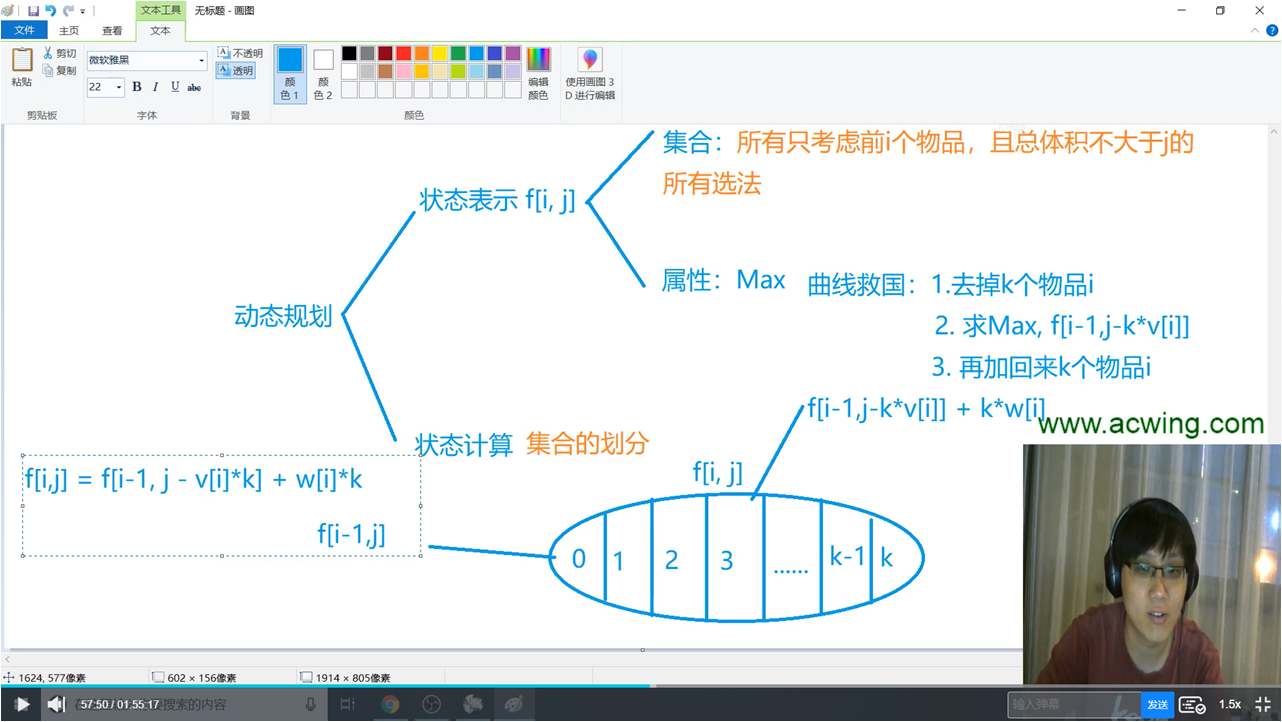
状态f[i][j]定义：前i个物品，背包容量j下的最优解（最大价值）

import java.util.*;

public class Main {

    static final int N = 1010;
    static int[][] f = new int[N][N];
    static int[] v = new int[N], w = new int[N];
    static int n, m;

    public static void main(String[] args) {

        Scanner sc = new Scanner(System.in);

        n = sc.nextInt();
        m = sc.nextInt();

        for (int i = 1; i <= n; i++) {
            v[i] = sc.nextInt();
            w[i] = sc.nextInt();
        }

        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++) {
                f[i][j] = f[i - 1][j];
                if (j >= v[i]) f[i][j] = Math.max(f[i][j], f[i - 1][j - v[i]] + w[i]);
            }

        System.out.println(f[n][m]);
    }
}

一维优化 ：

https://www.acwing.com/solution/content/1374/

明确一维数组的含义f[j]表示容量为j的背包，价值的最大值是多少发现无论背包是否能放下，都会使用上一层的数据进行更新本层数据，这里我们记上一层为one，本层为second

对于second来说，想要使用one的数据来更新f数组只能逆序遍历f
原因如下：
如果顺序遍历的话,语句：f[j] = Math.min(f[j], f[j - v[i]] + w[i])显然f[j]是one的数据，但是对于f[j - v[i]],由于我们是顺序的，因此在此之前f[j - v[i]]的数据就已经被更新过了，换句话说就是这时候f[j - v[i]]的数据是second的数据。
逆序遍历的话，f[j]明显还是one的数据，考虑f[j - v[i]]，由于我们是逆序遍历，所有j - v[i] < j,因此在f[j]之前并没有更新f[j - v[i]],也就是说f[j - v[i]]还是属于one的数据，此时我们在使用f[j] = Math.min(f[j], f[j - v[i]] + w[i])语句就是在使用one的数据进行更新second的数据

因此这里需要逆序遍历

借鉴别人题解图片

优化代码

import java.util.*;

public class Main {
    static final int N = 1010;
    static int[] f = new int[N];
    static int n, m;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        n = sc.nextInt();
        m = sc.nextInt();

        while (n -- > 0) {

            int v = sc.nextInt(), w = sc.nextInt();
            for (int j = m; j >= v; j--) 
                f[j] = Math.max(f[j], f[j - v] + w);
        }        

        System.out.println(f[m]);
    }
}

完全背包

题目： https://www.acwing.com/problem/content/3/

朴素

import java.util.*;

public class Main {

    static final int N = 1010;
    static int[][] f = new int[N][N];
    static int[] v = new int[N], w = new int[N];
    static int n, m;

    public static void main(String[] args) {

        Scanner sc = new Scanner(System.in);

        n = sc.nextInt();
        m = sc.nextInt();

        for (int i = 1; i <= n; i++) {
            v[i] = sc.nextInt();
            w[i] = sc.nextInt();
        }

        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                for (int k = 0; k * v[i] <= j; k++) {
                    f[i][j] = Math.max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
                }
            }
        }
        System.out.println(f[n][m]);
    }
}

数学推导优化

将

        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                for (int k = 0; k * v[i] <= j; k++) {
                    f[i][j] = Math.max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
                }
            }
        }

优化为

        for (int i = 1; i <= n; i ++) {
            for (int j = 1; j <= m; j++) {
                f[i][j] = f[i - 1][j];
                if (v[i] <= j) f[i][j] = Math.max(f[i][j], f[i][j - v[i]] + w[i]);
            }
        }

全部代码

import java.util.*;

public class Main {

    static final int N = 1010;
    static int[][] f = new int[N][N];
    static int[] v = new int[N], w = new int[N];
    static int n, m;

    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);

        n = sc.nextInt();
        m = sc.nextInt();

        for (int i = 1; i <= n; i++) {
            v[i] = sc.nextInt();
            w[i] = sc.nextInt();
        }

        for (int i = 1; i <= n; i ++) {
            for (int j = 1; j <= m; j++) {
                f[i][j] = f[i - 1][j];
                if (v[i] <= j) f[i][j] = Math.max(f[i][j], f[i][j - v[i]] + w[i]);
            }
        }

        System.out.println(f[n][m]);
    }
}

优化为一维

代码

f[i][j] = f[i - 1][j];
if (v[i] <= j) f[i][j] = Math.max(f[i][j], f[i][j - v[i]] + w[i]);

只是使用了本层数据并没有使用上一层数据(对于数据f[i - 1][j]，本层和上一层的数据在操作时是一样的)
因此直接删除第一维度正序遍历即可

代码如下

import java.util.*;

public class Main {

    static final int N = 1010;
    static int[] f = new int[N];
    static int[] v = new int[N], w = new int[N];
    static int n, m;

    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);

        n = sc.nextInt();
        m = sc.nextInt();

        for (int i = 1; i <= n; i++) {
            v[i] = sc.nextInt();
            w[i] = sc.nextInt();
        }

        for (int i = 1; i <= n; i ++)
            for (int j = 1; j <= m; j++)
                if (v[i] <= j) f[j] = Math.max(f[j], f[j - v[i]] + w[i]);

        System.out.println(f[m]);
    }
}

多重背包1 https://www.acwing.com/problem/content/4/

import java.util.*;

public class Main {

    static final int N = 110;
    static int[][] f = new int[N][N];
    static int[] v = new int[N], w = new int[N], s = new int[N];
    static int n, m;

    public static void main(String[] args) {

        Scanner sc = new Scanner(System.in);

        n = sc.nextInt();
        m = sc.nextInt();

        for (int i = 1; i <= n; i++) {
            v[i] = sc.nextInt();
            w[i] = sc.nextInt();
            s[i] = sc.nextInt();
        }

        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                for (int k = 0; s[i] >= k && k * v[i] <= j; k++) {
                    f[i][j] = Math.max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
                }
            }
        }
        System.out.println(f[n][m]);
    }
}

多重背包2(对1的优化) https://www.acwing.com/problem/content/5/

二进制优化
使用1, 2, 4, 8, …, 512可以凑出来0~1023之间的所有数字(每个数是选与不选)
(也可以用十进制的数字都可以使用二进制来表示进行理解)

即对于任意一个S(物品的个数) 找到一个k满足1 + 2 + 4 + …+ 2^k + c = S(c为常数且c = 2^(k+1)-S)

未优化

import java.util.*;
import java.io.*;

public class Main{
    static final int N = 12 * 1000, M = 2010;
    static int[][] f = new int[N][M];
    static int[] v = new int[N], w = new int[N];
    static int cnt, n, m;

    public static void main(String[] args) throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        String[] str = br.readLine().split(" ");
        n = Integer.parseInt(str[0]);
        m = Integer.parseInt(str[1]);

        for (int i = 1; i <= n; i ++) {
            str = br.readLine().split(" ");

            int a = Integer.parseInt(str[0]), b = Integer.parseInt(str[1]), c = Integer.parseInt(str[2]);
            int k = 1;
            while (k <= c) {
                cnt++;
                v[cnt] = a * k;
                w[cnt] = b * k;
                c -= k;
                k *= 2;
            }

            if (c > 0) {
                cnt++;
                v[cnt] = c * a;
                w[cnt] = c * b;
            }
        }    

        n = cnt;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                f[i][j] = f[i - 1][j];
                if (v[i] <= j) f[i][j] = Math.max(f[i][j], f[i - 1][j - v[i]] + w[i]);
            }
        }

        System.out.println(f[n][m]);
    }
}

优化为一维度(同01)

import java.util.*;

public class Main{

    static final int N = 15000;
    static int[] f = new int[N], v = new int[N], w = new int[N];
    static int cnt, n, m;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        n = sc.nextInt();
        m = sc.nextInt();

        for (int i = 1; i <= n; i ++) {
            int a = sc.nextInt(), b = sc.nextInt(), c = sc.nextInt();
            int k = 1;
            while (k <= c) {
                cnt++;
                v[cnt] = a * k;
                w[cnt] = b * k;
                c -= k;
                k *= 2;
            }

            if (c > 0) {
                cnt++;
                v[cnt] = c * a;
                w[cnt] = c * b;
            }
        }    

        n = cnt;
        for (int i = 1; i <= n; i++) {
            for (int j = m; j >= v[i]; j--) {
                f[j] = Math.max(f[j], f[j - v[i]] + w[i]);
            }
        }

        System.out.println(f[m]);
    }
}

分组背包 https://www.acwing.com/problem/content/9/

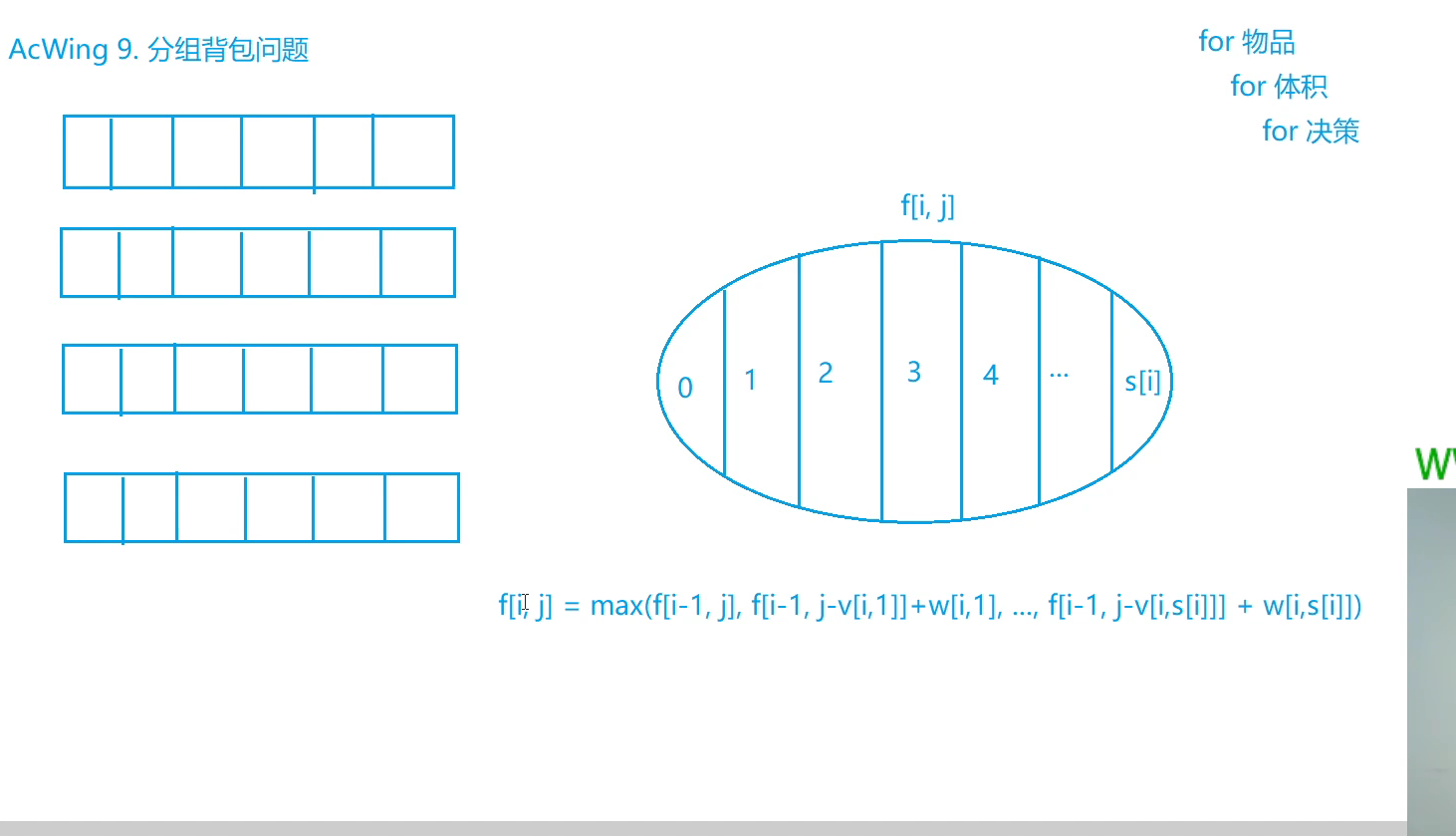
import java.util.*;

public class Main {

    static final int N = 110;
    static int[][] f = new int[N][N], v = new int[N][N], w = new int[N][N];
    static int[] s = new int[N];
    static int n, m;

    public static void main(String[] args) {

        Scanner sc = new Scanner(System.in);

        n = sc.nextInt();
        m = sc.nextInt();

        for (int i = 1; i <= n; i++) {
            s[i] = sc.nextInt();
            for (int j = 1; j <= s[i]; j++) {
                v[i][j] = sc.nextInt();
                w[i][j] = sc.nextInt();
            }
        }

        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                f[i][j] = f[i - 1][j];
                for (int k = 1; k <= s[i]; k++) {
                    if (v[i][k] <= j)
                        f[i][j] = Math.max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);
                }
            }
        }

        System.out.println(f[n][m]);
    }
}

混合背包

https://www.acwing.com/solution/content/261656/

有依赖的背包

https://www.acwing.com/solution/content/261704/

背包问题求方案数(最大价值)

https://www.acwing.com/solution/content/261730/

背包的方案记录

01背包记录

import java.util.*;
import java.io.*;

public class Main {
    static final int N = 1010;
    static PrintWriter out = new PrintWriter(System.out);
    static int[][] f = new int[N][N];
    static int[] v = new int[N], w = new int[N];
    static int n, m;

    public static void main(String[] args) {

        Scanner sc = new Scanner(System.in);

        String[] str = sc.nextLine().split(" ");
        n = Integer.parseInt(str[0]);
        m = Integer.parseInt(str[1]);

        for (int i = 1; i <= n; i++) {
            str = sc.nextLine().split(" ");
            v[i] = Integer.parseInt(str[0]);
            w[i] = Integer.parseInt(str[1]);
        }

        for (int i = n; i >= 1; i--)
            for (int j = 1; j <= m; j++) {
                f[i][j] = f[i + 1][j];
                if (j >= v[i])
                    f[i][j] = Math.max(f[i][j], f[i + 1][j - v[i]] + w[i]);
            }
        int j = m;
        for (int i = 1; i <= n; i++)
            if (j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i]) {
                out.print(i + " ");
                j -= v[i];
            }
        out.flush();
    }
}

深搜版本dfs

import java.util.*;
import java.io.*;

public class Main {
    static final int N = 1010;
    static PrintWriter out = new PrintWriter(System.out);
    static int[][] f = new int[N][N];
    static int[] v = new int[N], w = new int[N];
    static int n, m;

    public static void main(String[] args) {

        Scanner sc = new Scanner(System.in);

        String[] str = sc.nextLine().split(" ");
        n = Integer.parseInt(str[0]);
        m = Integer.parseInt(str[1]);

        for (int i = 1; i <= n; i++) {
            str = sc.nextLine().split(" ");
            v[i] = Integer.parseInt(str[0]);
            w[i] = Integer.parseInt(str[1]);
        }

        for (int i = n; i >= 1; i--)
            for (int j = 1; j <= m; j++) {
                f[i][j] = f[i + 1][j];
                if (j >= v[i])
                    f[i][j] = Math.max(f[i][j], f[i + 1][j - v[i]] + w[i]);
            }
        dfs(1, m);
        out.flush();
    }

    static void dfs(int i, int j) {
        if (i > n || j <= 0) return;

        if (j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i]) {
            out.print(i + " ");
            dfs(i + 1, j - v[i]);
        } else dfs(i + 1, j);
    }
}