一

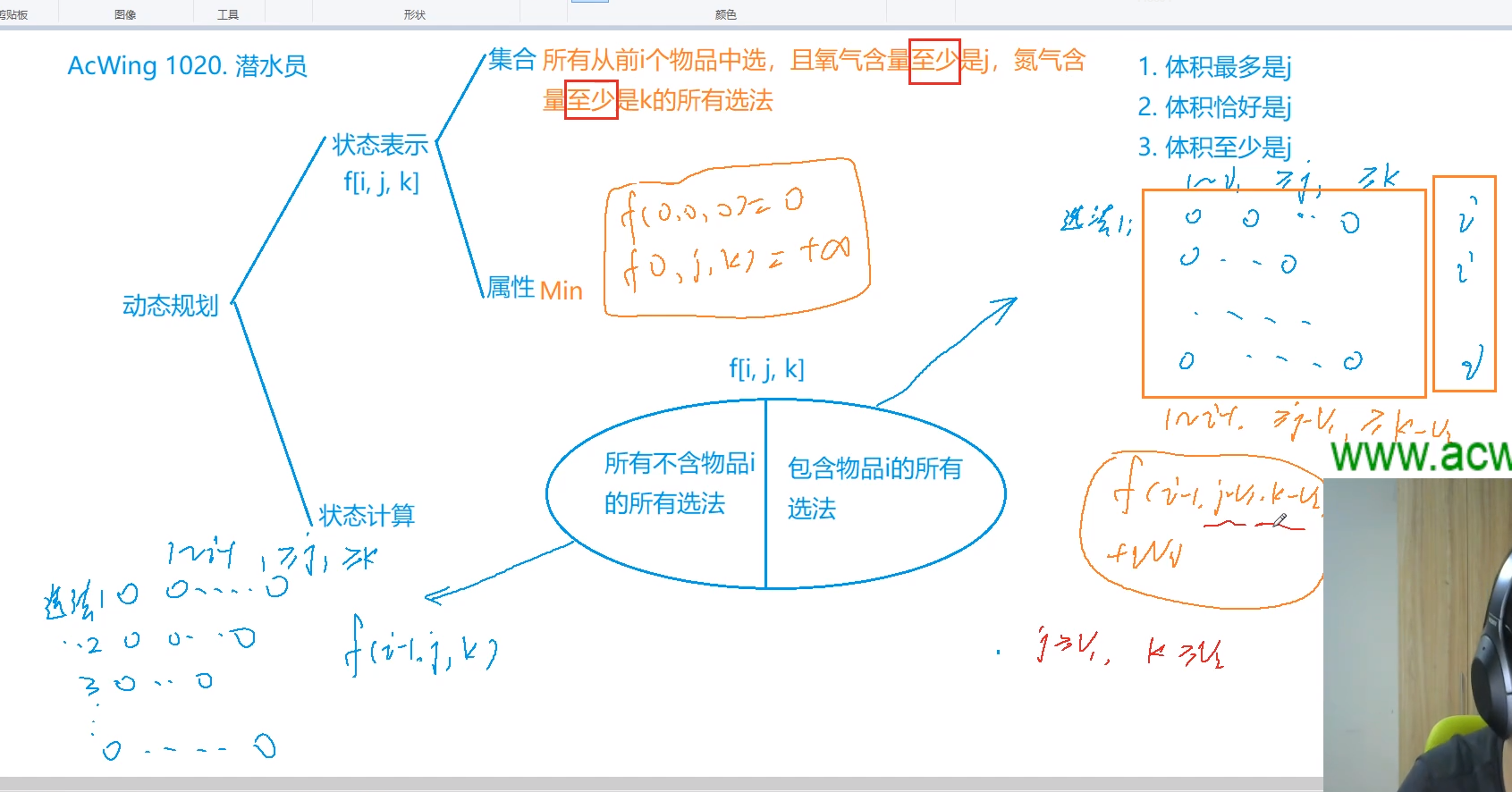
f[i][j][k] 表示考虑前i个物品，花费代价1至少为j，花费代价2
至少为k时的最小重量
初始化全部为INF，f[0][0][0] = 0(考虑0个物品)

import java.util.*;

public class Main {
    static final int N = 1010, INF = 0x3f3f3f3f;;
    static int[][][] f = new int[N][50][160];
    static int[] y = new int[N], d = new int[N], q = new int[N];
    static int m, n, k;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        String[] str = sc.nextLine().split(" ");
        m = Integer.parseInt(str[0]);
        n = Integer.parseInt(str[1]);
        k = Integer.parseInt(sc.nextLine());

        for (int i = 1; i <= k; i++) {
            str = sc.nextLine().split(" ");
            y[i] = Integer.parseInt(str[0]);
            d[i] = Integer.parseInt(str[1]);
            q[i] = Integer.parseInt(str[2]);
        }

        for (int i = 0; i < N; i++)
            for (int j = 0; j < 50; j++) Arrays.fill(f[i][j], INF);
        f[0][0][0] = 0;

        for (int i = 1; i <= k; i++)
            //j和k必须从0开始遍历，氧气和氮气没有的情况也需要考虑
            for (int j = 0; j <= m; j++)
                for (int t = 0; t <= n; t++) {
                    int t1 = j - y[i], t2 = t - d[i];
                    //当y[i] > j时也满足条件，通过0来转移状态(考虑f的状态表示)
                    if (t1 < 0) t1 = 0;
                    if (t2 < 0) t2 = 0;
                    f[i][j][t] = Math.min(f[i - 1][j][t], f[i - 1][t1][t2] + q[i]);
                }

        System.out.println(f[k][m][n]);
    }
}

一的第二种写法(更易理解)

import java.util.*;

public class Main {
    static final int N = 1010, INF = 0x3f3f3f3f;;
    static int[][][] f = new int[N][50][160];
    static int[] y = new int[N], d = new int[N], q = new int[N];
    static int m, n, k;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        String[] str = sc.nextLine().split(" ");
        m = Integer.parseInt(str[0]);
        n = Integer.parseInt(str[1]);
        k = Integer.parseInt(sc.nextLine());

        for (int i = 1; i <= k; i++) {
            str = sc.nextLine().split(" ");
            y[i] = Integer.parseInt(str[0]);
            d[i] = Integer.parseInt(str[1]);
            q[i] = Integer.parseInt(str[2]);
        }

        for (int i = 0; i < N; i++)
            for (int j = 0; j < 50; j++) Arrays.fill(f[i][j], INF);
        f[0][0][0] = 0;

        for (int i = 1; i <= k; i++)
            for (int j = 0; j <= m; j++)
                for (int t = 0; t <= n; t++) {
                    int v1 = y[i], v2 = d[i], w = q[i];
                    //不选择i号物品
                    f[i][j][t] = f[i - 1][j][t];
                    //分情况讨论

                    //物品i加上就够一维使用，此时，只关心二维情况即可
                    if (j < v1 && t >= v2) 
                        f[i][j][t] = Math.min(f[i - 1][0][t - v2] + w, f[i][j][t]);
                    //物品i加上就够二维使用，此时，只关心一维情况即可
                    else if (j >= v1 && t < v2) 
                        f[i][j][t] = Math.min(f[i - 1][j - v1][0] + w, f[i][j][t]);
                    //如果选择了i号物品，两个维度直接拉满，那么只选择一个i就足够用，它参选的价值是w
                    else if (j < v1 && t < v2) 
                        f[i][j][t] = Math.min(f[i][j][t], w);
                    //正常递推
                    else 
                        f[i][j][t] = Math.min(f[i][j][t], f[i - 1][j - v1][t - v2] + w);
                }

        System.out.println(f[k][m][n]);
    }
}