首先我们要确定son[N][2]中N的大小，题目中“所有 bi以及 ci加起来的和不超过 5×10^5”,而bi和ci是每个序列的长度，我们在建trie树时，是依据每次传入的加密序列，也就是说我们最多可能新增（加密序列的个数）*bi个节点，因此最多会有5×10^5个节点，所以这里N取5×10^5。（这里不太确定！）

样例

4 1
3 0 1 0
1 1
3 1 0 0
3 1 1 0
2 0 1

1、m_n数组什么时候加，我们在建trie树时，在每个加密序列的结尾用m_n[加密序列结尾对应的idx]，统计加密序列的结尾，方便后续我们统计加密序列中是解密序列的前缀的个数（解密序列长度>=加密序列）。
2、n_m数组什么时候加，而n_m数组统计的则是每个加密序列经过的节点，每有一个加密序列经过一个节点，n_m[经过节点对应的idx],最后n_m[解密序列的结尾对应节点的idx]表示的就是加密序列中，以解密序列为前缀的个数（加密序列长度>=解密序列长度）。
3、在查询返回时，我们使用ret进行统计，在根据解密序列访问trie树时，有三种情况：

1、加密序列在解密序列到达末尾前结束，也就是m_n[对应节点idx]的值
2、解密序列中在根据加密序列建好的trie树中找不到对应节点，就代表后续不会有以解密序列为前缀的加密序列，解密序列中也不会再包含后续的加密序列，此时我们直接return ret即可
3、解密序列到达末尾，这时我们需要统计加密序列大于解密序列这个集合中，经过解密序列结尾对应节点的加密序列个数，也就是n_m[解密序列结尾对应结尾idx]的值，但有可能某个加密序列和解密序列完全相同，我们在统计解密序列经过的节点时已经统计，因此需要减去一次m_n[解密序列结尾对应结尾idx]。

如下图，为上述样例的trie树

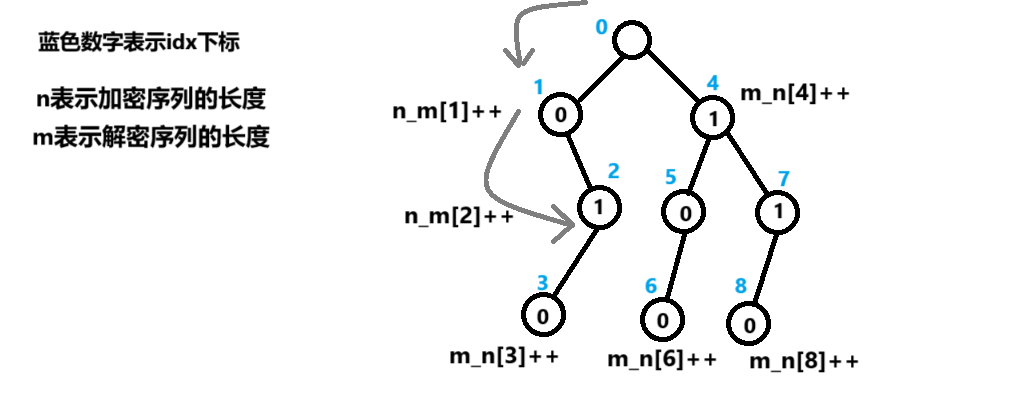
我们只要统计m_n[1]+m_n[2]+n_m[2]

C++ 代码

#include <iostream>
#include <vector>
using namespace std;
const int N=5*1e5+10;

int n,m;
int son[N][2];
int idx;
//m表示解密长度，n表示加密长度，m_n表示m>=n
int m_n[N];
//n>=m
int n_m[N];
void insert(vector<int>& a)
{
    int p=0;
    for(int i=0;i<a.size();i++)
    {
        int u=a[i];
        if(!son[p][u])
            son[p][u]=++idx;
        p=son[p][u];
        //统计解密字符串当加密字符串的前缀
        n_m[p]++;   
    }
    //统计加密字符串当解密字符串的前缀
    m_n[p]++;
}
int query(vector<int>& a)
{
    int p=0;
    int ret=0;
    for(int i=0;i<a.size();i++)
    {
        int u=a[i];
        if(!son[p][u])
            return ret;
        p=son[p][u];
        ret+=m_n[p];
    }
    return ret+n_m[p]-m_n[p];
}
int main()
{
    cin>>n>>m;
    for(int i=0;i<n;i++)
    {
        int t;
        cin>>t;
        vector<int> a(t);
        for(int j=0;j<t;j++)
        {
            cin>>a[j];
        }
        insert(a);
    }
    while(m--)
    {
        int t;
        cin>>t;
        vector<int> a(t);
        for(int j=0;j<t;j++)
        {
            cin>>a[j];
        }   

        cout<<query(a)<<endl;   
    }
    return 0;
}