对原题进行抽象：

有一个长为$ n $的数组$ a $

定义一个集合$ S $，若$ x\in S $，则数组$ a $中至少有$ x $个数大于等于$ x $

现在你有$ m $次修改机会，可以将$ a_i $修改成$ a_i+1 $，但每个元素最多只能进行一次修改

求$ max\;S $

输入格式：

$ n\;m $

$ a_1 \; a_2 \; … \; a_n $

数据范围：

$ 1\le n\le 10^5 $
$ 0 \le m \le 10^5 $
$ 0 \le a_i \le 10^5 $

思路一：二分答案

若本题答案为$ ans $，则说明给我们$ m $次修改机会，我们有能力使数组$ a $中至少有$ ans $个数大于等于$ ans $

如果我们有能力使数组$ a $中至少有$ ans $个数大于等于$ ans $，那么我们一定也可以使数组$ a $中至少有$ ans-1 $个数大于等于$ ans-1 $(这是显然的，不是嘛)

由此，我们发现了一个很好的二分性质，因此我们可以进行二分答案来解决这道题

用图来表示划分为：

二分答案的两个关键：边界和$ check $函数的实现

边界：

本题我们可以设置边界$ [0,n] $来二分答案，因为若$ x \in S $，则$ 0 \le x \le n $

(小于等于$ n $是肯定的，因为数组$ a $的长度固定为$ n $)

(大于等于$ 0 $也是肯定的，因为数组$ a $的数都是非负的，则至少有$ 0 $个数大于等于$ 0 $，$ 0 \in S $。且根据实际意义，集合$ S $中的元素肯定都是非负的，因此$ 0 $自然成了$ S $中的最小值，$ min \; S = 0 $）

$ check $函数的实现：

定义$ check(mid) $为：判断给定$ m $次修改机会，是否有能力使数组$ a $中至少有$ mid $个数大于等于$ mid $

实现：

维护两个变量，记$ u $为数组$ a $中大于等于$ mid $的数的个数，记$ v $为数组$ a $中恰好等于$ mid-1 $的数的个数。

那若给我们$ m $次修改机会，则数组$ a $中最多有$ u+min(v,m) $个数大于等于$ mid $

我们判断$ u+min(v,m) $是否大于等于$ mid $即可实现$ check $函数

即$ check(mid) \Leftrightarrow u+min(v,m) \ge mid $

(注意：“有$ u+min(v,m) $个数大于等于$ mid $”和“$ u+min(v,m) $是否大于等于$ mid $”是有区别的，别搞晕了hh)

代码：

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
const int N=1e5+10;
int a[N];
int n,m;
bool check(int mid){
    //u:数组a中大于等于mid的数的个数
    //v:数组a中恰好等于mid-1的数的个数
    int u=0,v=0;
    for(int i=1;i<=n;i++){
        if(a[i]>=mid) u++;
        else if(a[i]==mid-1) v++;
    }
    return u+min(v,m)>=mid;
}
void solve(){
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];

    int l=0,r=n;
    while(l<r){
        int mid=l+(r-l+1>>1);//l=mid的话要多加1
        if(check(mid)) l=mid;
        else r=mid-1;
    }
    cout<<r<<endl;
}
void FileIO() {
    freopen("test.in","r",stdin);
    freopen("test.out","w",stdout);
}
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(0);

    //FileIO();
    int t = 1;
    //cin >> t;
    for(int i=1;i<=t;i++){
        solve();
    }
    return 0;
}

然后其实还能这么写，这个感觉$check$函数更直接明了一些
代码：

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
const int N=1e5+10;
int a[N];
int n,m;
bool check(int mid) {
    int cnt=0;//能大于等于mid的数的个数
    int chance=m;//修改机会
    for(int i=1; i<=n; i++) {
        if(a[i]>=mid) {
            cnt++;
        } else if(a[i]==mid-1) {
            if(chance) {//如果a[i]为mid-1且我们还要修改机会
                cnt++;
                chance--;
            }
        }
    }
    return cnt>=mid;//判断
}
void solve() {
    cin>>n>>m;
    for(int i=1; i<=n; i++) cin>>a[i];

    int l=0,r=n;
    while(l<r) {
        int mid=l+(r-l+1>>1);
        if(check(mid)) l=mid;
        else r=mid-1;
    }
    cout<<r<<endl;
}
void FileIO() {
    freopen("test.in","r",stdin);
    freopen("test.out","w",stdout);
}
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(0);

    //FileIO();
    int t = 1;
    //cin >> t;
    for(int i=1; i<=t; i++) {
        solve();
    }
    return 0;
}

思路二：双指针

首先$ 0 $肯定是$ S $中的一个元素了，我们尝试在$ [1,n] $从大到小枚举$ i $，若发现$ i \in S $，则答案肯定为$ i $(这就是上面讲过的二分的性质)

怎么判断$ i $是否是$ S $中的元素呢？

首先将数组$ a $从大到小排个序，则

$ i \in S \Leftrightarrow a_i \ge i-1 且 a_{1…i}中最多有m个数等于i-1 $

$ a_i \ge i-1 $是极其好判断的，关键在于，怎么判断$ a_{1…i}中最多有m个数等于i-1 $

诶，写到这里，在一个有序数组中查找某元素的个数不是用$ lower\_bound $和$ upper\_bound $快速实现吗？写到这里，我立马去试了试这种写法，代码如下：

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
const int N=1e5+10;
int a[N];
int n,m;
void solve(){
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];
    sort(a+1,a+n+1,greater<int>());//排序

    int ans=0;//答案
    for(int i=n;i>=1;i--){
        //这里还要稍微注意一下,因为lower_bound和upper_bound是默认在非递减序列上工作的
        //我们要传一个greater<int>(),告诉lower_bound和upper_bound现在是在非递增序列上工作
        if(a[i]>=i-1&& upper_bound(a+1,a+i+1,i-1,greater<int>())-lower_bound(a+1,a+i+1,i-1,greater<int>()) <= m){
            ans=i;
            break;
        }
    }
    cout<<ans<<endl;
}
void FileIO() {
    freopen("test.in","r",stdin);
    freopen("test.out","w",stdout);
}
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(0);

    //FileIO();
    int t = 1;
    //cin >> t;
    for(int i=1;i<=t;i++){
        solve();
    }
    return 0;
}

发现是能过的。

hh

用$ lower\_bound $和$ upper\_bound $感觉挺无脑的hh

我们尝试练练思维，想想用其他的方式来判断$ a_{1…i}中最多有m个数等于i-1 $

接下来介绍正式的双指针思路：

我们定义$ j=f(i) $为：从左往右第一个小于$ i $的数的下标

我们发现，$ f(i) $是关于$ i $的单调函数

可以这样朴素的揭示：

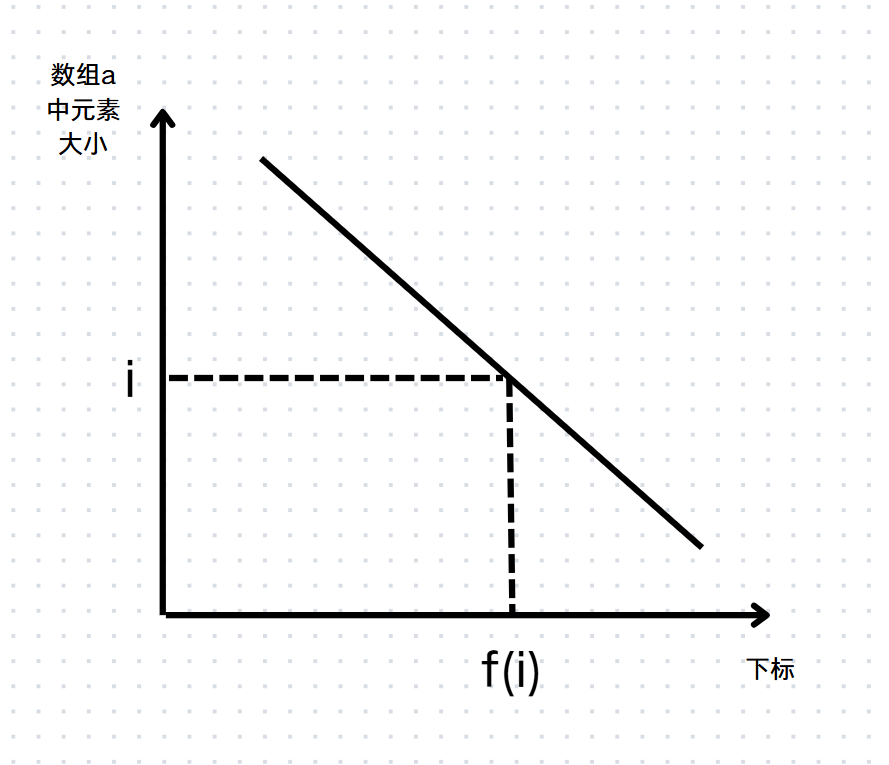
既然$ j $关于$ i $单调，那么我们可以用双指针来维护$ j $

维护$ j $的用处在于，$ a_{1…i}中等于i-1的数的个数就是i-j+1 $

代码：

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
const int N=1e5+10;
int a[N];
int n,m;
void solve(){
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];
    sort(a+1,a+n+1,greater<int>());//从大到小排序

    int ans=0;//答案
    for(int i=n,j=1;i>=1;i--){
        while(j<=n&&a[j]>=i) j++;//j是第一个小于i的数
        if(a[i]>=i-1&&i-j+1<=m){//判断
            ans=i;
            break;
        }
    }
    cout<<ans<<endl;
}
void FileIO() {
    freopen("test.in","r",stdin);
    freopen("test.out","w",stdout);
}
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(0);

    //FileIO();
    int t = 1;
    //cin >> t;
    for(int i=1;i<=t;i++){
        solve();
    }
    return 0;
}