import java.util.*;

public class Main {
    static final int N = 110;
    static int[][] f = new int[N][N];
    static int[] h = new int[N], e = new int[N], ne = new int[N];
    static int[] v = new int[N], w = new int[N];
    static int n, m, idx = 0;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        n = sc.nextInt();
        m = sc.nextInt();

        Arrays.fill(h, -1);
        int root = -1;
        for (int i = 1; i <= n; i++) {
            int a = sc.nextInt(), b = sc.nextInt(), father = sc.nextInt();
            v[i] = a;
            w[i] = b;
            //i的父节点是father
            if (father != -1) add(father, i);
            else root = i;
        }

        dfs(root);
        System.out.println(f[root][m]);
    }

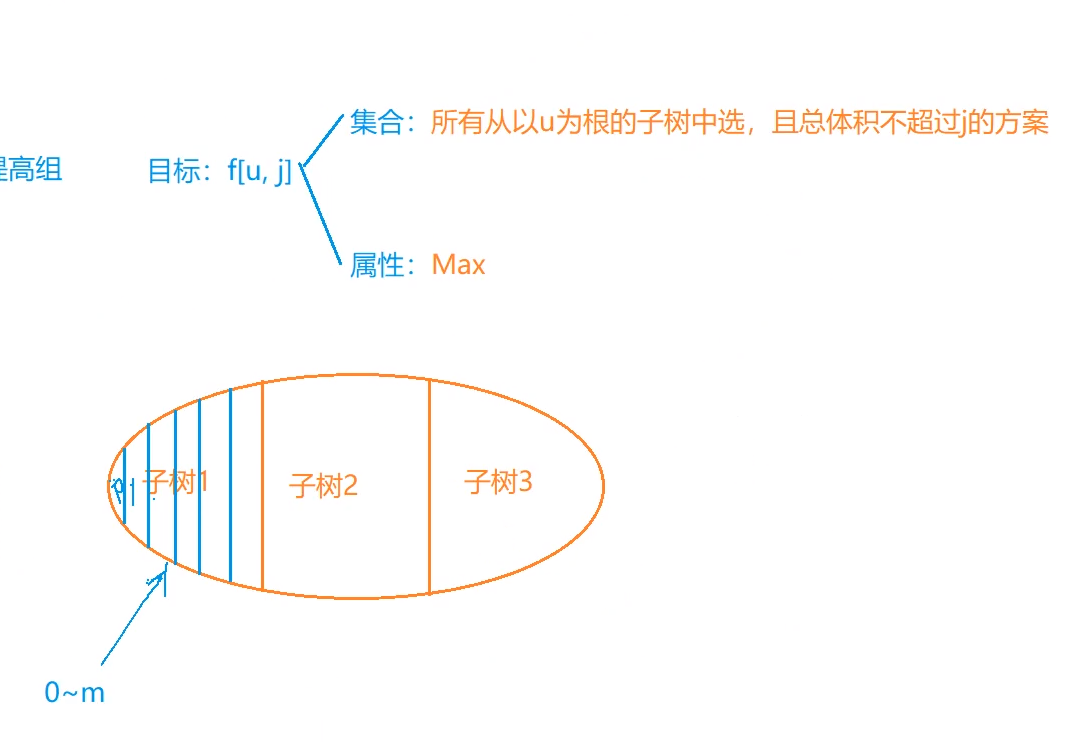
    //f[i][j]表示以i为根的节点的花费j的最大价值
    static void dfs(int u) {
        for (int i = h[u]; i != -1; i = ne[i]) {
            int son = e[i];
            dfs(son);
            //枚举所有要被更新的状态，子树的总体积为j = m - v[u]最后再选择(树根是必选的)
            for (int j = m - v[u]; j >= 0; j--)
                /*
                这个时候当前结点我们看成是分组背包中的一个组，
                子节点的每一种选择我们都看作是组内一种物品
                */
                for (int k = 0; k <= j; k++)//遍历子节点的在体积j的组合(递推)
                    f[u][j] = Math.max(f[u][j], f[u][j - k] + f[son][k]);
        }

        //最后选上第u件物品
        for (int j = m; j >= v[u]; j--) f[u][j] = f[u][j - v[u]] + w[u];
        //体积不足v[u]就选不上树根那么下面的子树就也不用选择了
        for (int j = 0; j < v[u]; j++) f[u][j] = 0;
    }

    //a向b连边
    static void add(int a, int b) {
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx++;
    }
}