题目描述

给你一个长度为 n 的整数数组 nums 和一个 正 整数 threshold。

有一张 n 个节点的图，其中第 i 个节点的值为 nums[i]。如果两个节点对应的值满足 lcm(nums[i], nums[j]) <= threshold，那么这两个节点在图中有一条 无向 边连接。

请你返回这张图中 连通块 的数目。

一个 连通块 指的是一张图中的一个子图，子图中任意两个节点都存在路径相连，且子图中没有任何一个节点与子图以外的任何节点有边相连。

lcm(a, b) 的意思是 a 和 b 的 最小公倍数。

样例

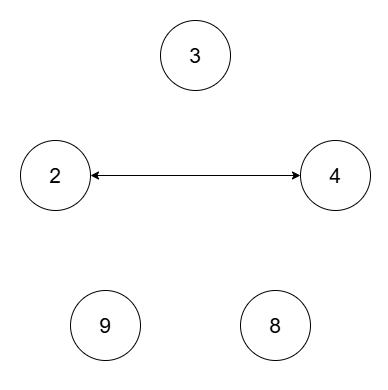
输入：nums = [2,4,8,3,9], threshold = 5

输出：4

解释：

四个连通块分别为 (2, 4)，(3)，(8)，(9)。

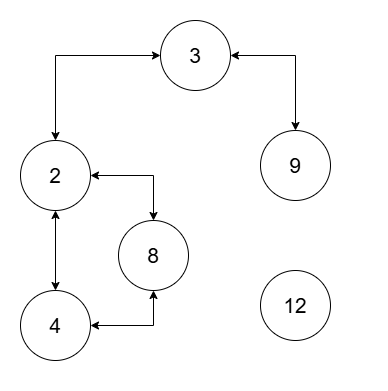
输入：nums = [2,4,8,3,9,12], threshold = 10

输出：2

解释：

两个连通块分别为 (2, 3, 4, 8, 9) 和 (12)。

限制

• 1 <= nums.length <= 10^5
• 1 <= nums[i] <= 10^9
• nums 中所有元素互不相同。
• 1 <= threshold <= 2 * 10^5

算法

(并查集) $O(n + threshold \log threshold)$

1. 遍历所有的数字，并把每个数字和它的倍数通过并查集连接，直到倍数达到 $threshold$。
2. 如果某个数字超过了 $threshold$，则不操作并查集，答案直接累加 $1$。
3. 遍历每个小于 $threshold$ 的数字，统计这些数字所占的连通块的个数，累加到答案中。

时间复杂度

• 并查集单次操作的时间复杂度近似为常数。
• 遍历所有数字和它的倍数，由于所有数字互不相同，则总的时间复杂度不超过 $O(n + threshold \log threshold)$。
• 累加答案的时间复杂度为 $O(n)$。
• 故总时间复杂度为 $O(n + threshold \log threshold)$。

空间复杂度

• 需要 $O(threshold)$ 的额外空间存储并查集。

C++ 代码

class Solution {
private:
    vector<int> f, sz;

    int find(int x) {
        return x == f[x] ? x : f[x] = find(f[x]);
    }

    void add(int x, int y) {
        int fx = find(x), fy = find(y);
        if (fx == fy)
            return;

        if (sz[fx] < sz[fy]) {
            f[fx] = fy;
            sz[fy] += sz[fx];
        } else {
            f[fy] = fx;
            sz[fx] += sz[fy];
        }
    }

public:
    int countComponents(vector<int>& nums, int threshold) {
        f.resize(threshold + 1);
        sz.resize(threshold + 1, 1);

        for (int i = 1; i <= threshold; i++)
            f[i] = i;

        int ans = 0;
        for (int x : nums) {
            if (x > threshold) ++ans;
            else {
                for (int i = x + x; i <= threshold; i += x)
                    add(i, x);
            }
        }

        unordered_set<int> h;
        for (int x : nums)
            if (x <= threshold && h.find(find(x)) == h.end()) {
                ++ans;
                h.insert(find(x));
            }

        return ans;
    }
};