题目描述

给你一个数组 points，其中 points[i] = [x_i, y_i] 表示无限平面上一点的坐标。

你的任务是找出满足以下条件的矩形可能的 最大 面积：

• 矩形的四个顶点必须是数组中的 四个 点。
• 矩形的内部或边界上 不能 包含任何其他点。
• 矩形的边与坐标轴 平行。

返回可以获得的 最大面积，如果无法形成这样的矩形，则返回 -1。

样例

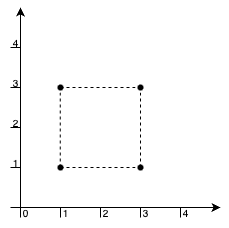
输入： points = [[1,1],[1,3],[3,1],[3,3]]

输出：4

解释：

我们可以用这 4 个点作为顶点构成一个矩形，并且矩形内部或边界上没有其他点。
因此，最大面积为 4 。

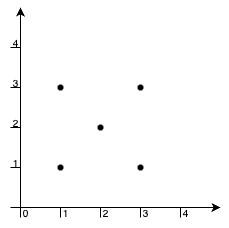
输入： points = [[1,1],[1,3],[3,1],[3,3],[2,2]]

输出：-1

解释：

唯一一组可能构成矩形的点为 [1,1], [1,3], [3,1] 和 [3,3]，但点 [2,2] 总是位于矩形内部。
因此，返回 -1 。

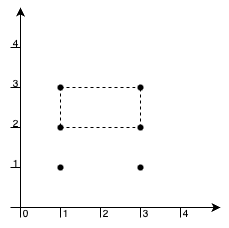
输入： points = [[1,1],[1,3],[3,1],[3,3],[1,2],[3,2]]

输出：2

解释：

点 [1,3], [1,2], [3,2], [3,3] 可以构成面积最大的矩形，面积为 2。
此外，点 [1,1], [1,2], [3,1], [3,2] 也可以构成一个符合题目要求的矩形，面积相同。

限制

• 1 <= points.length <= 10
• points[i].length == 2
• 0 <= x_i, y_i <= 100
• 给定的所有点都是 唯一 的。

算法

(暴力枚举，哈希表) $O(n^3)$

1. 枚举点对，并判断这个点对构成的矩形是否存在另外两个点。
2. 如果能构成矩形，则枚举所有的点，保证没有其他点在这个矩形中。

时间复杂度

• 将所有点存入哈希表的时间复杂度为 $O(n)$。
• 枚举点对的时间复杂度为 $O(n^2)$，每次判断的时间复杂度为 $O(n)$。
• 故总时间复杂度为 $O(n^3)$。

空间复杂度

• 需要 $O(n)$ 的额外空间存储哈希表。

C++ 代码

class Solution {
public:
    int maxRectangleArea(vector<vector<int>>& points) {
        const int n = points.size();

        unordered_set<string> h;

        for (const auto &p : points)
            h.insert(to_string(p[0]) + "," + to_string(p[1]));

        auto check = [&](int x0, int y0, int x1, int y1) {
            if (x0 > x1) swap(x0, x1);
            if (y0 > y1) swap(y0, y1);

            for (const auto &p : points) {
                if ((p[0] == x0 || p[0] == x1) && (p[1] == y0 || p[1] == y1))
                    continue;

                if (x0 <= p[0] && p[0] <= x1 && y0 <= p[1] && p[1] <= y1)
                    return false;
            }

            return true;
        };

        int ans = -1;
        for (int i = 0; i < n; i++)
            for (int j = i + 1; j < n; j++) {
                int x0 = points[i][0], y0 = points[i][1];
                int x1 = points[j][0], y1 = points[j][1];

                if (x0 == x1 || y0 == y1)
                    continue;

                if (h.find(to_string(x0) + "," + to_string(y1)) == h.end())
                    continue;

                if (h.find(to_string(x1) + "," + to_string(y0)) == h.end())
                    continue;

                if (check(x0, y0, x1, y1))
                    ans = max(ans, abs(x0 - x1) * abs(y0 - y1));
            }


        return ans;
    }
};