题目描述

在无限平面上有 n 个点。给定两个整数数组 xCoord 和 yCoord，其中 (xCoord[i], yCoord[i]) 表示第 i 个点的坐标。

你的任务是找出满足以下条件的矩形可能的 最大 面积：

• 矩形的四个顶点必须是数组中的 四个 点。
• 矩形的内部或边界上 不能 包含任何其他点。
• 矩形的边与坐标轴 平行。

返回可以获得的 最大面积，如果无法形成这样的矩形，则返回 -1。

样例

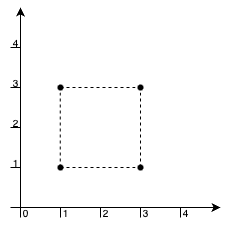
输入： xCoord = [1,1,3,3], yCoord = [1,3,1,3]

输出： 4

解释：

我们可以用这 4 个点作为顶点构成一个矩形，并且矩形内部或边界上没有其他点。

因此，最大面积为 4。

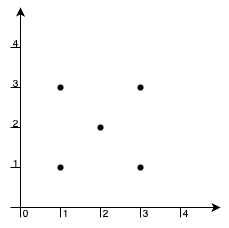
输入： xCoord = [1,1,3,3,2], yCoord = [1,3,1,3,2]

输出： -1

解释：

唯一一组可能构成矩形的点为 [1,1], [1,3], [3,1] 和 [3,3]，但点 [2,2] 总是位于矩形内部。

因此，返回 -1。

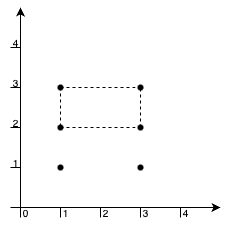
输入： xCoord = [1,1,3,3,1,3], yCoord = [1,3,1,3,2,2]

输出： 2

解释：

点 [1,3], [1,2], [3,2], [3,3] 可以构成面积最大的矩形，面积为 2。

此外，点 [1,1], [1,2], [3,1], [3,2] 也可以构成一个符合题目要求的矩形，面积相同。

限制

• 1 <= xCoord.length == yCoord.length <= 2 * 10^5
• 0 <= xCoord[i], yCoord[i] <= 8 * 10^7
• 给定的所有点都是 唯一 的。

算法

(扫描线，有序集) $O(n \log n)$

1. 先把所有点按照 x 轴从小到大排序，同一个 x 坐标的，按照 y 坐标从小到大排序。
2. 遍历每一个 x 坐标，遍历相邻的 y 坐标组成的线段。在这个过程中，维护一个有序集，存储纵向的线段与 x 坐标的映射。
3. 遍历线段时，如果当前线段出现在有序集中，则更新答案。
4. 然后遍历每一个单独的 y 坐标，删除包含当前 y 坐标的所有线段。
5. 最后将当前 x 坐标的所有线段插入到有序集中。

时间复杂度

• 排序的时间复杂度为 $O(n \log n)$。
• 遍历坐标时，每个点/线段最多进集合一次，出集合一次。
• 故总时间复杂度为 $O(n \log n)$。

空间复杂度

• 需要 $O(n)$ 的额外空间存储排序的下标，排序的系统栈和有序集。

C++ 代码

#define LL long long

class Solution {
public:
    LL maxRectangleArea(vector<int>& xCoord, vector<int>& yCoord) {
        const int n = xCoord.size();

        vector<int> p(n);
        for (int i = 0; i < n; i++)
            p[i] = i;

        sort(p.begin(), p.end(), [&](int x, int y) {
            if (xCoord[x] != xCoord[y])
                return xCoord[x] < xCoord[y];

            return yCoord[x] < yCoord[y];
        });

        map<pair<int, int>, int> seg;
        LL ans = -1;

        for (int i = 1, j = 0; i <= n; i++) {
            if (i < n && xCoord[p[i]] == xCoord[p[j]])
                continue;

            int x = xCoord[p[j]];
            for (int k = j; k < i - 1; k++) {
                auto s = make_pair(yCoord[p[k]], yCoord[p[k + 1]]);

                auto it = seg.find(s);
                if (it != seg.end())
                    ans = max(ans, (LL)(s.second - s.first) * (x - it->second));
            }

            for (int k = j; k < i; k++) {
                int y = yCoord[p[k]];

                while (!seg.empty()) {
                    auto it = seg.upper_bound(make_pair(y, INT_MAX));
                    if (it == seg.begin())
                        break;

                    --it;
                    if (y <= it->first.second) seg.erase(it);
                    else break;
                }
            }

            for (int k = j; k < i - 1; k++)
                seg[make_pair(yCoord[p[k]], yCoord[p[k + 1]])] = x;

            j = i;
        }

        return ans;
    }
};