高斯消元解线性方程组

题目描述
$ \color {white} {} $
输入一个包含 $n$ 个方程 $n$ 个未知数的线性方程组。
$ \color {white} {} $
方程组中的系数为实数。
$ \color {white} {} $
求解这个方程组。
$ \color {white} {} $
下图为一个包含 $m$ 个方程 $n$ 个未知数的线性方程组示例：

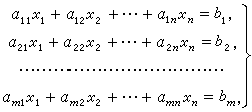
输入格式

第一行包含整数 $n$。
$ \color {white} {我是占位符，看不见我} $
接下来 $n$ 行，每行包含 $n$+$1$ 个实数，表示一个方程的 $n$ 个系数以及等号右侧的常数。

输出格式

如果给定线性方程组存在唯一解，则输出共 $n$ 行，其中第 $i$ 行输出第 $i$ 个未知数的解，结果保留两位小数。
$ \color {white} {我是占位符，看不见我} $
注意：本题有 SPJ，当输出结果为 0.00 时，输出 -0.00 也会判对。在数学中，一般没有正零或负零的概念，所以严格来说应当输出 0.00，但是考虑到本题作为一道模板题，考察点并不在于此，在此处卡住大多同学的代码没有太大意义，故增加 SPJ，对输出 -0.00 的代码也予以判对。
$ \color {white} {我是占位符，看不见我} $
如果给定线性方程组存在无数解，则输出 Infinite group solutions。
$ \color {white} {我是占位符，看不见我} $
如果给定线性方程组无解，则输出 No solution。

数据范围

$1≤n≤100$
所有输入系数以及常数均保留两位小数，绝对值均不超过 $100$。

输入样例：

3
1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1.00 -1.00 2.00 7.00

输出样例：

1.00
-2.00
3.00

前置

初等行列变换

1.把某一行乘一个非$0$的数 (方程的两边同时乘上一个非$0$数不改变方程的解)
$ \color {white} {} $
2.交换某两行 (交换两个方程的位置)
$ \color {white} {} $
3.把某行的若干倍加到另一行上去（把一个方程的若干倍加到另一个方程上去）
$ \color {white} {} $

判断有无唯一解

唯一解如果矩阵完成操作之后呈完美阶梯型，则有唯一解。
$ \color {white} {} $
无解如果通过方程推出非0=0，则无解
$ \color {white} {} $
无穷多组解如果通过方程推出0=0,则有无穷多组解
$ \color {white} {} $

高斯消元的步骤

1找到绝对值最大的一行（为了代码的稳定性）
$ \color {white} {} $
2将该行移到最上面
$ \color {white} {} $
3将该行第一个数变为$1$
$ \color {white} {} $
4将最上面一行下面所有行的第$c$
列变成$0$
$ \color {white} {} $
知道了以上的前置知识点，就可以写代码了

代码

#include <bits/stdc++.h>
using namespace std;
double eps = 1e-8;
int n;
double a[105][105];
int gauss(){
    int r,c;
    for(r = 0,c = 0; c < n; c ++){
        int t = c;
        for(int i = r; i < n; i ++){
            if(fabs(a[i][c]) > fabs(a[t][c])) t = i;
        }
        if(fabs(a[t][c]) < eps) continue;
        for(int i = c; i <= n; i ++) swap(a[t][i],a[r][i]);
        for(int i = n; i >= c;  i --){
            a[r][i] /= a[r][c];
        }
        for(int i = r + 1; i < n; i ++){
            if(fabs(a[i][c]) > eps){
                for(int j = n; j >= c; j --) a[i][j] -= a[r][j] * a[i][c];
            }
        }
        r ++;
    }
    if(r < n){
        for(int i = r; i < n; i ++){
            if(fabs(a[i][n]) > eps) return 2;
        }
        return 1;
    }
    for(int i = n - 1; i >= 0; i --){
        for(int j = i + 1; j < n; j ++){
            a[i][n] -= a[j][n] * a[i][j];
        }
    }
    return 0;
}
int main(){
    cin >> n;
    for(int i = 0; i < n; i ++) {
        for(int j = 0; j <= n; j ++) cin >> a[i][j];
    }
    int t = gauss();
    if(t == 2) puts("No solution");
    else if(t == 1) puts("Infinite group solutions");
    else {
        for(int i = 0; i < n; i ++){
            cout << fixed << setprecision(2) << a[i][n] << endl;
        }
    }
    return 0;
}