状压dp经典题目：最短Hamilton路径

传送门:最短Hamilton路径

首先考虑选择路径其中的规律和性质
起点和终点都是定好的，中间如何走，我们无法确定

假如有4个点，我们可以有以下走法
$0-1-2-3$设结果为4
$0-2-1-3$设结果为5

我们发现，中间如何走，我们根本就不用关心，因为我们求的是经过所有点后的最短路径

我们只需要关心最后的结果，谁小，我们就选谁

于是，dp分析图如下

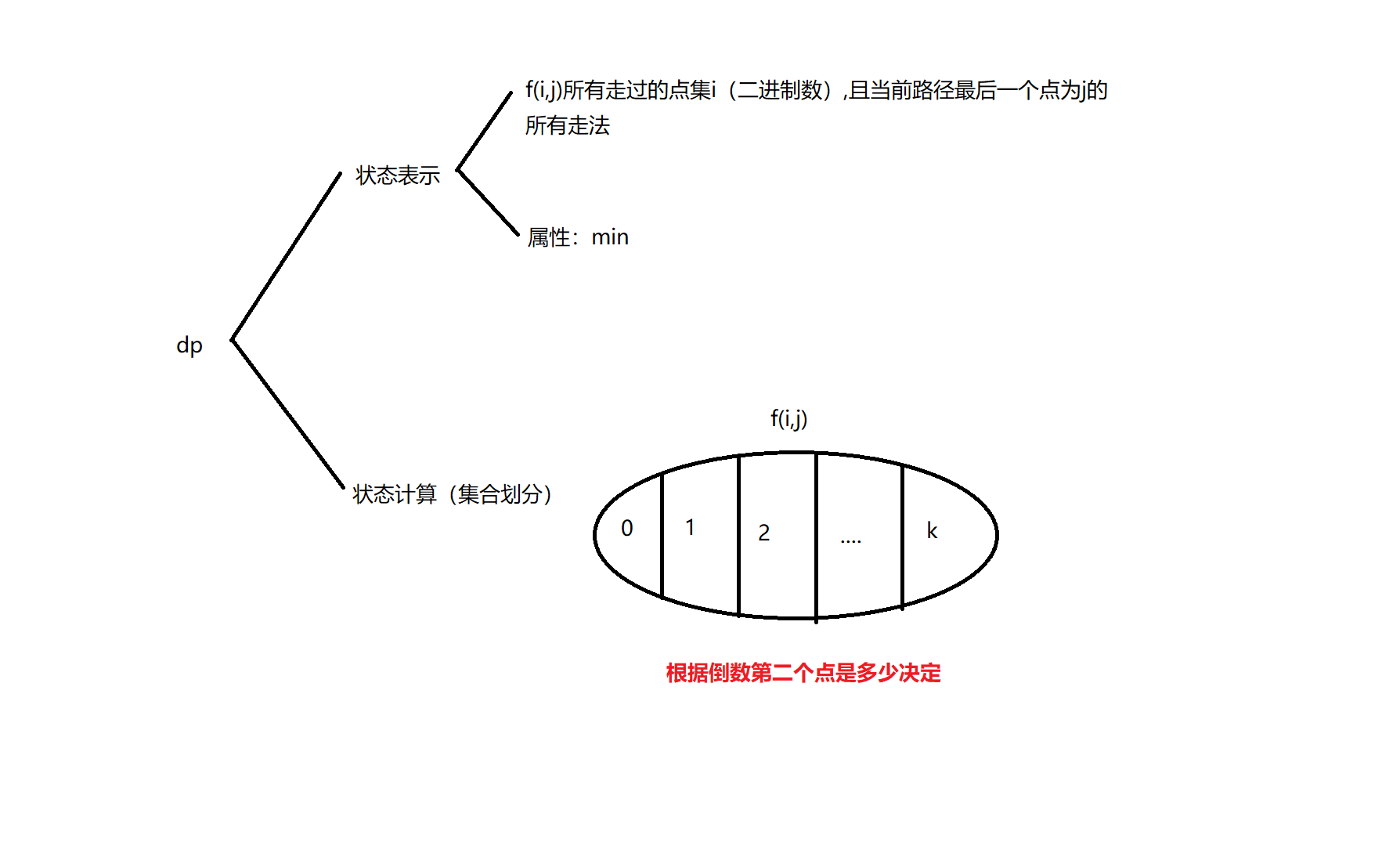
总结一些细节问题：
这里的i是一个二进制数，是一个点集，如果当前路径经过了这个点，就置为1.否则，为0
例如：

设当前路径为0->3 ，总共5个点，i总位数为5，经过0,3，所以第0和第三位为1
表示为：10100

由于$f(i,j)$我们不确定，所以我们需要借助$j$前面的点$k$，来进行状态转移

如何进行状态转移

设当前状态为$f(i,j)$j前面的点为$k$

路径就形如以下形式
$0\to....\to k\to j$

如果我们要利用k来计算j，那么，从上面路径可以得到一个性质

如果要得到从$0$到$k$的路径，那么从$0$到$k$的路径中，不能包含$j$

需要通过位运算去掉$k$点集中包含$j$的点集

i^(1<<j)就能从i点集中去掉第j个点，将其设置为0

那么，只需要求出，从0到k再加上从k到j的距离的最小值即可

具体细节请参见代码

参考题解

最短Hamilton路径

非常感谢！

代码实现

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 20,M=1<<20;
int n;
int a[N][N],f[M][N];

const int INF=0x3f3f3f3f;

//f表示所有i点集中，最后一个点为j的走法，状态转移依据:考虑倒数第二个点k的情况
int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++)
        {
            scanf("%d", &a[i][j]);
        }
    }

    memset(f,INF,sizeof f);//求最小值，所以初始值设为正无穷
    f[1][0]=0;//初始状态从0出发，最后一个点为0，状态为1，表示只经过0号点

    for(int i=0;i<(1<<n);i++)
    {
        for(int j=0;j<n;j++)//枚举倒数第一个点j
        {
            if(i>>j&1)//判断j是不是存在，不存在不符合状态转移要求，跳过
            {
                for(int k=0;k<n;k++)//枚举倒数第二个点k
                {
                    if((i^(1<<j))>>k&1)//去掉j后如果k仍在在点集中才进行转移
                    {
                        f[i][j]=min(f[i][j],f[i^(1<<j)][k]+a[k][j]);
                    }
                }
            }
        }
    }

    cout<<f[(1<<n)-1][n-1]<<endl;//经过所有点（1111..111）且最后一个点为n-1为最终结果

    return 0;
}