题目描述

给你一个 m x n 的二维数组 grid，数组由 正整数 组成。

你的任务是以 之字形 遍历 grid，同时跳过每个 交替 的单元格。

之字形遍历的定义如下：

• 从左上角的单元格 (0, 0) 开始。
• 在当前行中向 右 移动，直到到达该行的末尾。
• 下移到下一行，然后在该行中向 左 移动，直到到达该行的开头。
• 继续在行间交替向右和向左移动，直到所有行都被遍历完。

注意：在遍历过程中，必须跳过每个 交替 的单元格。

返回一个整数数组 result，其中包含按 顺序 记录的、且跳过交替单元格后的之字形遍历中访问到的单元格值。

样例

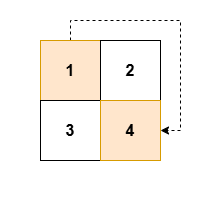
输入： grid = [[1,2],[3,4]]

输出： [1,4]

解释：

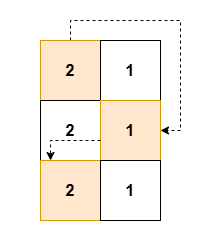
输入： grid = [[2,1],[2,1],[2,1]]

输出： [2,1,2]

解释：

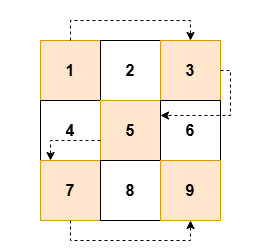
输入： grid = [[1,2,3],[4,5,6],[7,8,9]]

输出： [1,3,5,7,9]

解释：

限制

• 2 <= n == grid.length <= 50
• 2 <= m == grid[i].length <= 50
• 1 <= grid[i][j] <= 2500

算法

(暴力枚举) $O(mn)$

1. 按照题目描述的模拟遍历，当 $i+j$ 为偶数时，放到 $result$ 中。

时间复杂度

• 遍历二维数组一次，时间复杂度为 $O(mn)$。

空间复杂度

• 需要 $O(mn)$ 的额外空间存储答案。

C++ 代码

class Solution {
public:
    vector<int> zigzagTraversal(vector<vector<int>>& grid) {
        const int m = grid.size(), n = grid[0].size();

        vector<int> result;

        for (int i = 0; i < m; i++) {
            if (i & 1) {
                for (int j = n - 1; j >= 0; j--)
                    if (!((i + j) & 1))
                        result.push_back(grid[i][j]);
            } else {
                for (int j = 0; j < n; j++)
                    if (!((i + j) & 1))
                        result.push_back(grid[i][j]);
            }
        }

        return result;
    }
};