题目描述

给你两个整数 n 和 threshold，同时给你一个 n 个节点的 有向 带权图，节点编号为 0 到 n - 1。这个图用 二维 整数数组 edges 表示，其中 edges[i] = [A_i, B_i, W_i] 表示节点 A_i 到节点 B_i 之间有一条边权为 W_i 的有向边。

你需要从这个图中删除一些边（也可能 不 删除任何边），使得这个图满足以下条件：

• 所有其他节点都可以到达节点 0。
• 图中剩余边的 最大 边权值尽可能小。
• 每个节点都 至多 有 threshold 条出去的边。

请你返回删除必要的边后，最大 边权的 最小值 为多少。如果无法满足所有的条件，请你返回 -1。

样例

输入：n = 5, edges = [[1,0,1],[2,0,2],[3,0,1],[4,3,1],[2,1,1]], threshold = 2

输出：1

解释：

删除边 2 -> 0 。剩余边中的最大值为 1 。

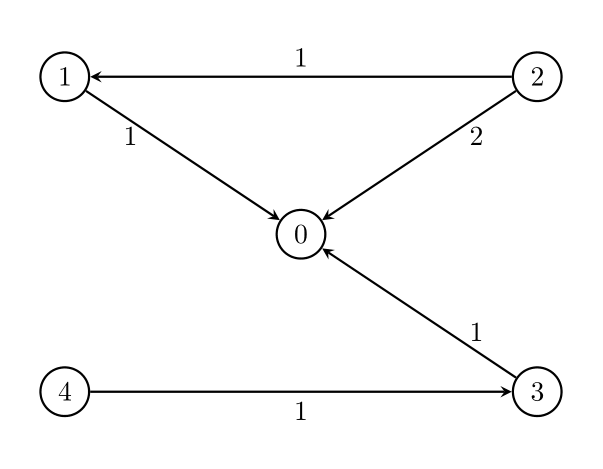
输入：n = 5, edges = [[0,1,1],[0,2,2],[0,3,1],[0,4,1],[1,2,1],[1,4,1]], threshold = 1

输出：-1

解释：

无法从节点 2 到节点 0。

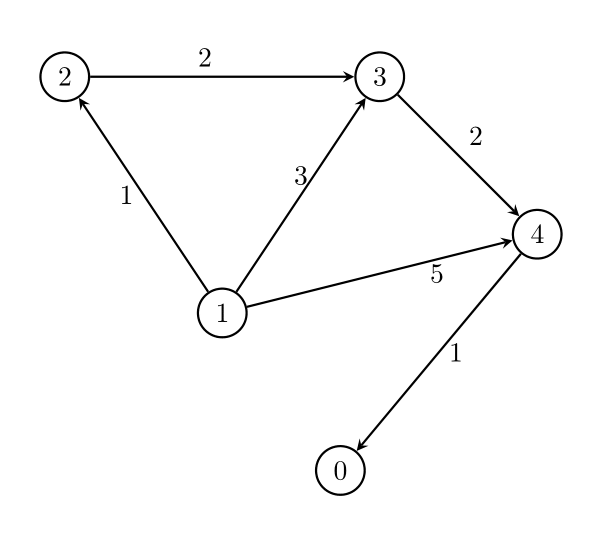
输入：n = 5, edges = [[1,2,1],[1,3,3],[1,4,5],[2,3,2],[3,4,2],[4,0,1]], threshold = 1

输出：2

解释：

删除边 1 -> 3 和 1 -> 4。剩余边中的最大值为 2。

输入：n = 5, edges = [[1,2,1],[1,3,3],[1,4,5],[2,3,2],[4,0,1]], threshold = 1

输出：-1

限制

• 2 <= n <= 10^5
• 1 <= threshold <= n - 1
• 1 <= edges.length <= min(10^5, n * (n - 1) / 2)
• edges[i].length == 3
• 0 <= A_i, B_i < n
• A_i != B_i
• 1 <= W_i <= 10^6
• 一对节点之间 可能 会有多条边，但它们的权值互不相同。

算法

(二分答案，宽度优先遍历) $O((m + n) \log U)$

1. 先二分边权的最大值，找到满足连通性的情况下的最大边权的最小值。
2. 可以通过在反图上宽度优先遍历来判定。
3. 找到最小值后，判定是否可以满足入度的要求（因为建反图了）。
4. 判定 threshold 也可以通过宽度优先遍历，标记使用的边，最后统计是否满足条件。

时间复杂度

• 二分判定的时间复杂度为 $O(m + n)$，故总时间复杂度为 $O((m + n) \log U)$。

空间复杂度

• 需要 $O(n + m)$ 的额外空间存储邻接表，队列和标记数组。

C++ 代码

const int N = 100010, INF = 1000001;

struct Edge {
    int to, w, nxt;
    bool used;

    Edge(){}

    Edge(int to_, int w_, int nxt_) {
        to = to_; w = w_; nxt = nxt_; used = false;
    }
};

class Solution {
private:
    int head[N], graphmr;
    Edge es[N];
    bool seen[N];
    queue<int> q;

    void add(int x, int y, int w) {
        int p = ++graphmr;
        es[p] = Edge(y, w, head[x]);
        head[x] = p;
    }

    bool check_conn(int p, int n) {
        memset(seen, false, n * sizeof(bool));
        seen[0] = true;
        q.push(0);

        while (!q.empty()) {
            int u = q.front();
            q.pop();

            for (int i = head[u]; i; i = es[i].nxt)
                if (es[i].w <= p && !seen[es[i].to]) {
                    q.push(es[i].to);
                    seen[es[i].to] = true;
                }
        }

        for (int i = 0; i < n; i++)
            if (!seen[i])
                return false;

        return true;
    }

    bool check_threshold(int p, int n, int threshold) {
        memset(seen, false, n * sizeof(bool));
        seen[0] = true;
        q.push(0);

        while (!q.empty()) {
            int u = q.front();
            q.pop();

            for (int i = head[u]; i; i = es[i].nxt)
                if (!seen[es[i].to]) {
                    es[i].used = true;
                    q.push(es[i].to);
                    seen[es[i].to] = true;
                }
        }

        vector<int> indegree(n, 0);
        for (int i = 0; i < n; i++)
            for (int j = head[i]; j; j = es[j].nxt)
                if (es[j].used)
                    ++indegree[es[j].to];

        for (int i = 0; i < n; i++)
            if (indegree[i] > threshold)
                return false;

        return true;
    }

public:
    int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
        memset(head, 0, n * sizeof(int));
        for (const auto &e : edges)
            add(e[1], e[0], e[2]);

        int l = 1, r = INF;
        while (l < r) {
            int mid = (l + r) >> 1;
            if (check_conn(mid, n)) r = mid;
            else l = mid + 1;
        }

        if (l == INF)
            return -1;

        if (!check_threshold(l, n, threshold))
            return -1;

        return l;
    }
};