引入

定义

给定一个 $n$ 行 $m$ 列的 01 矩阵，现在你需要挑选若干行，使得对于矩阵的每一列 $j$，在你挑选的这些行中，有且仅有一个 $1$。找到任意解。这个问题被称为精确覆盖问题。

例子

$$ \begin{pmatrix} 0 & 0 & 1 & 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 1 & 0 & 1 \end{pmatrix} $$

暴力

1

枚举每行是否被选择，时间复杂度 $O(n \times m \times 2^n)$。

2

将每行看做一个二进制数，因此问题转换为：选择若干个二进制数，使它们的按位与为 $0$，按位或为 $2^n-1$，$n$ 为选择二进制数的个数。枚举是否选择每个数，在搜索时判断即可做到 $O(2^n)$。

正解

暴力不可行，因此需要使用一种新的算法——Dancing Links 优化 X 算法，简称 DLX 算法。

X 算法

定义-相关元素

将 $x$ 行的所有元素打上标记，再将第 $x$ 行中含 $1$ 的列打上标记。所有打上标记的元素为 $x$ 行的相关元素。

将 $y$ 列的所有元素打上标记，再将第 $y$ 列中含 $1$ 的行打上标记。所有打上标记的元素为 $y$ 列的相关元素。

定义-强相关元素

将 $x$ 行的所有元素打上标记，将第 $x$ 行中含 $1$ 的列打上标记，再将上一步所有打上标记的列中含 $1$ 的行打上标记。所有打上标记的元素为 $x$ 行的强相关元素。

将 $y$ 列的所有元素打上标记，将第 $y$ 列中含 $1$ 的行打上标记，再将上一步所有打上标记的行中含 $1$ 的列打上标记。所有打上标记的元素为 $y$ 列的强相关元素。

算法步骤

1. 选择矩阵中未选择过的一行，设选中的这个行是 原来的 第 $x$ 行，将 $x$ 加入到答案集合 $S$ 中（这里我们统一按从第一行选择到最后一行选择）。如果所有行都已经尝试过，则判定为无解，算法结束。

2. 删除所有 $x$ 行的强相关元素。

3. 若新矩阵为不为空，则转到第一步。若新矩阵为空且 $x$ 行中的元素全部为 $1$，则找到答案，答案为需要选择集合 $S$ 中的所有行。若新矩阵为空且之前选择的行中元素不是全部为 $1$，则转到第一步并将所有 $x$ 的相关元素恢复。

例子

我们引用在精确覆盖问题中的例子来进行说明。

在这个例子中，我们先将这一行的所有强相关元素打上标记，再进行了删除操作。

初始矩阵为：

$$ \begin{pmatrix} 0 & 0 & 1 & 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 1 & 0 & 1 \end{pmatrix} $$

1. 选择第一行。红色为被选中行。

$$ \begin{pmatrix} \color{Red}0 & \color{Red}0 & \color{Red}1 & \color{Red}0 & \color{Red}1 & \color{Red}1 & \color{Red}0 \\ 1 & 0 & 0 & 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 1 & 0 & 1 \end{pmatrix} $$

1. 将第一行的所有相关元素打上标记，其中蓝色表示标记。

$$ \begin{pmatrix} \color{Blue}0 & \color{Blue}0 & \color{Blue}1 & \color{Blue}0 & \color{Blue}1 & \color{Blue}1 & \color{Blue}0 \\ 1 & 0 & \color{Blue}0 & 1 & \color{Blue}0 & \color{Blue}0 & 1 \\ \color{Blue}0 & \color{Blue}1 & \color{Blue}1 & \color{Blue}0 & \color{Blue}0 & \color{Blue}1 & \color{Blue}0 \\ 1 & 0 & \color{Blue}0 & 1 & \color{Blue}0 & \color{Blue}0 & 0 \\ 0 & 1 & \color{Blue}0 & 0 & \color{Blue}0 & \color{Blue}0 & 1 \\ \color{Blue}0 & \color{Blue}0 & \color{Blue}0 & \color{Blue}1 & \color{Blue}1 & \color{Blue}0 & \color{Blue}1 \end{pmatrix} $$

1. 删除所有被标记元素，得到一个新的小 01 矩阵：

$$ \begin{pmatrix} 1 & 0 & 1 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \end{pmatrix} $$

1. 选择第一行（注意，这个第一行是新矩阵的第一行，下面所有对于行的称呼均为当前矩阵的行数）。

$$ \begin{pmatrix} \color{Red}1 & \color{Red}0 & \color{Red}1 & \color{Red}1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \end{pmatrix} $$

1. 将第一行的所有相关元素打上标记。

$$ \begin{pmatrix} \color{Blue}1 & \color{Blue}0 & \color{Blue}1 & \color{Blue}1 \\ \color{Blue}1 & \color{Blue}0 & \color{Blue}1 & \color{Blue}0 \\ \color{Blue}0 & \color{Blue}1 & \color{Blue}0 & \color{Blue}1 \end{pmatrix} $$

1. 删除所有被标记元素，得到一个空矩阵。但是上次删除的行 1 0 1 1 不是全 $1$ 的，说明选择有误，需要回到 这个例子的 第 4 步重新选择。

2. 回溯到步骤 4，选择第二行。

$$ \begin{pmatrix} 1 & 0 & 1 & 1 \\ \color{Red}1 & \color{Red}0 & \color{Red}1 & \color{Red}0 \\ 0 & 1 & 0 & 1 \end{pmatrix} $$

1. 将第二行的所有相关元素打上标记。

$$ \begin{pmatrix} \color{Blue}1 & \color{Blue}0 & \color{Blue}1 & \color{Blue}1 \\ \color{Blue}1 & \color{Blue}0 & \color{Blue}1 & \color{Blue}0 \\ \color{Blue}0 & 1 & \color{Blue}0 & 1 \end{pmatrix} $$

1. 删除所有被标记元素，得到一个新的小 01 矩阵：

$$ \begin{pmatrix} 1 & 1 \end{pmatrix} $$

1. 选择第一行。

$$ \begin{pmatrix} \color{Red}1 & \color{Red}1 \end{pmatrix} $$

1. 将第二行的所有相关元素打上标记。

$$ \begin{pmatrix} \color{Blue}1 & \color{Blue}1 \end{pmatrix} $$

1. 删除所有被标记元素，得到一个空矩阵，且上一次删除的时候，删除的是全 $1$ 的行，算法结束，答案即为被选择的三行，即 $S$ 中的编号：$1, 4, 5$。

Dancing-Links 优化 X 算法（DLX 算法）

来源及基本思想

不难看出，X 算法需要大量的删除行、删除列和恢复行、恢复列的操作。

因此我们可以使用双十字链表维护。

而在双向十字链表上不断跳跃的过程被形象地比喻成跳跃，因此被用来优化 X 算法的双向十字链表也被称为 Dancing Links。

下文将介绍双十字链表的实现方式及 DLX 算法的实现方式。

时间复杂度

$O(x^n)$，其中 $n$ 为矩阵中 $1$ 的个数，$x$ 为一个非常接近于 $1$ 的常数。

双十字链表（Dancing Links）

定义

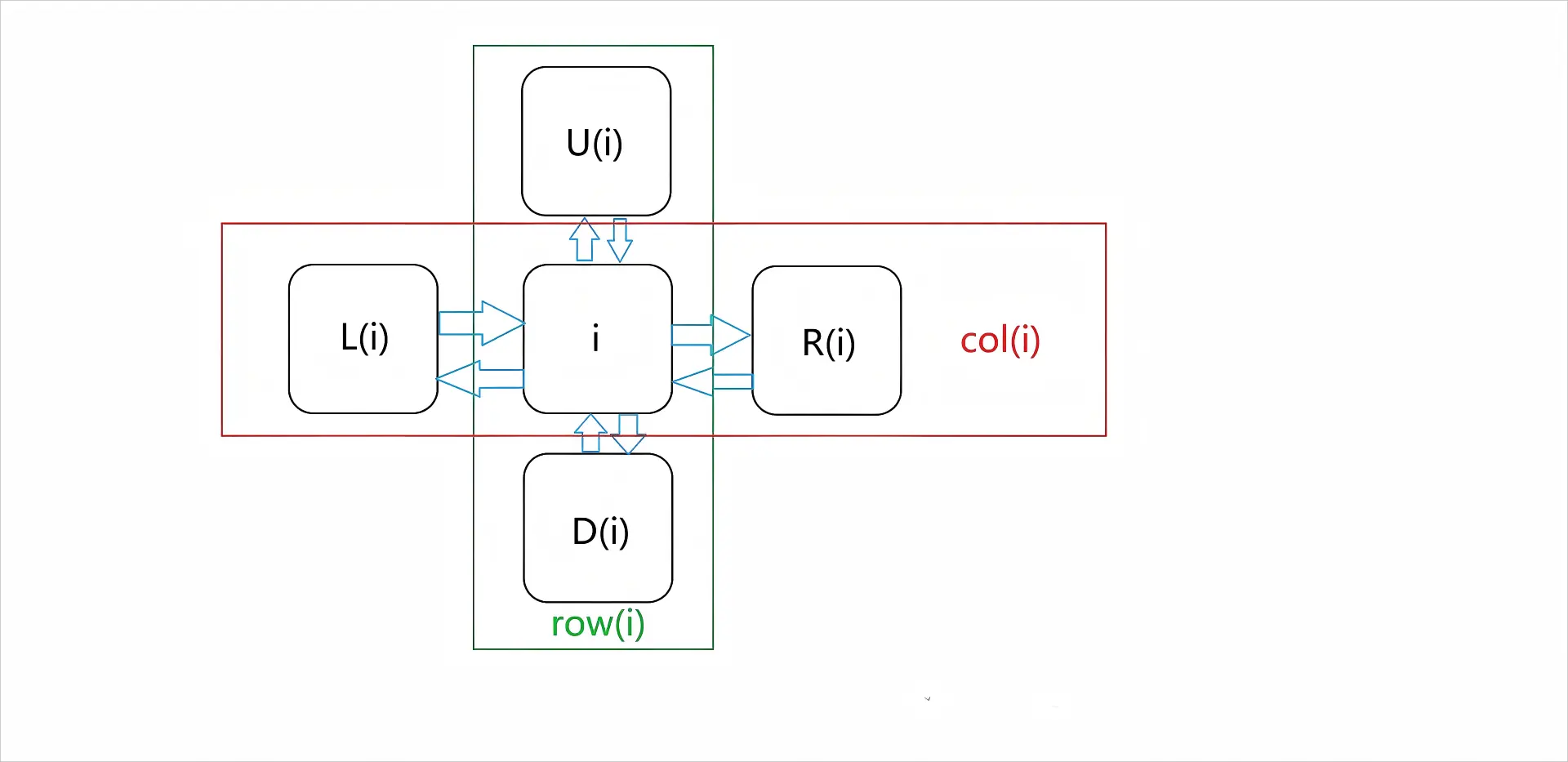
双十字链表不同于普通链表，它有 $4$ 个指针，分别指向上、下、左、右四个元素。如下图所示是双十字链表里的单个节点。

以下所有关于指针数组的描述与下图相同。

一整个双十字链表：

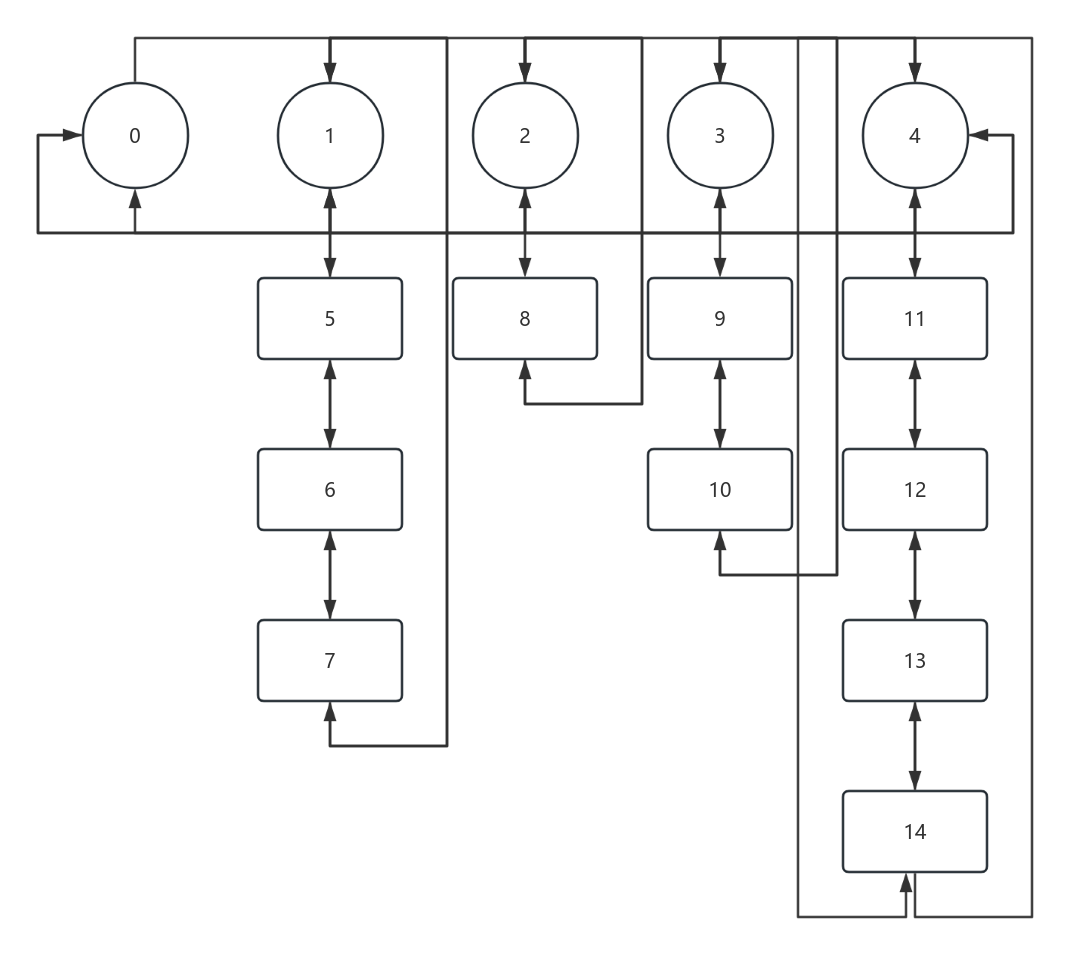
其中 $first$ 数组指向的是每行的开头，而在每列的开头有一个哨兵节点（图中白色节点），红色的 $0$ 号节点是双十字链表的初始节点。

操作

remove 操作

remove(x) 这个操作可以将第 $x$ 列的所有强相关元素移除。

注意：我们下文使用这个双十字链表时仅会插入为 $1$ 的位置，因此可以暴力删点。下同，不再赘述。

将第 $x$ 列移除仅需将其哨兵节点左右的节点连接即可。

接着枚举该列的所有结点，再枚举这些列所在的行，将这些行的所有节点的上下节点连接即可。

示例程序：

void remove(int x){
    //第x行的哨兵节点即为x节点。
    R[L[x]] = R[x];
    L[R[x]] = L[x];
    for(int y=U[x];y!=x;y=U[y]){
        for(int z=R[y];z!=y;z=R[z]){//因为每行都是双向循环链表，因此可以从任意这一行的一点开始遍历。
            U[D[z]] = U[z];
            D[U[z]] = D[z];
            sz[col[z]]--;//sz数组记录每列的元素个数，row_i表示i号元素属于哪一行，col_i表示i号元素属于哪一列，下同，并不再赘述。
        }
    }
}

recover 操作

remove(x) 这个操作可以将第 $x$ 列的所有强相关元素恢复。

这个操作即为 remove 操作的反向操作。

接着枚举该列的所有结点，再枚举这些列所在的行，将这些行的所有节点的上下节点连接到当前节点即可。

将第 $x$ 列移除仅需将其哨兵节点左右的节点连接到当前节点即可。

示例程序：

void recover(int x){
    for(int y=U[x];y!=x;y=U[y]){
        for(int z=R[y];z!=y;z=R[z]){
            U[D[z]] = z;
            D[U[z]] = z;
            sz[col[z]]++;
        }
    }
    R[L[x]] = x;
    L[R[x]] = x;
}

build 操作

build(r,c) 操作可以建一个新的长为 $r$，宽为 $c$ 的双十字链表。

我们仅需建出哨兵元素即可。

因为每一行都是双向循环链表，所以哨兵元素也不例外。

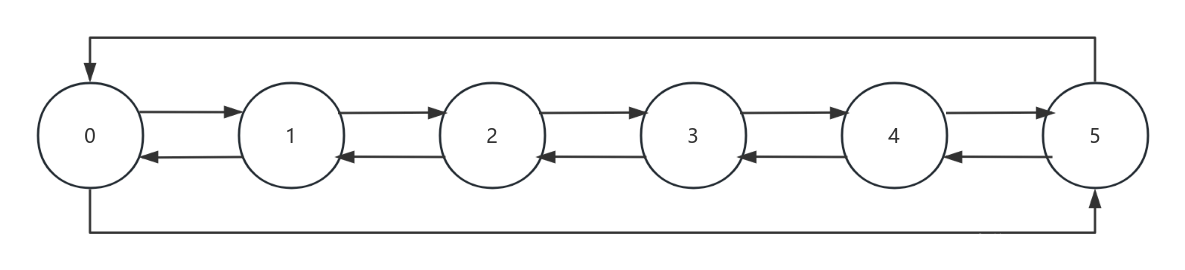
示例程序：

void build(int r,int c){
    n = r,m = c;//我们将双十字链表封装到结构体内，因此需要开设变量来保存边长。
    for(int i=0;i<=c;i++){//建立哨兵节点 
        L[i] = i-1,R[i] = i+1;
        U[i] = i,D[i] = i;//因为双十字链表的每一列也是双向循环链表，因此初始哨兵节点的上、下指针均指向自己。 
    }
  L[0] = c;
  R[c] = 0;
    id = c+1;//id表示如果要添加元素的话，下一个元素的编号，下文阐述插入操作时将会使用。
}

insert 操作

insert(r,c) 操作能在第 $r$ 行，第 $c$ 列的位置插入一个节点（这个节点编号为 $id$，上文示例程序的注释中有提到，这里不再赘述，下同）。

先设置这个节点的行（$row$ 数组）编号为 $r$，列（$col$ 数组）编号为 $c$。

然后将节点 $id$ 插入到第 $c$ 行哨兵节点下方，即 $c$ 节点下方。我们可以这样做是因为我们在删除与恢复操作时会遍历一整行或一整列，而每行或每列中元素顺序并不重要，下同，并不再赘述。

之后我们分两种情况讨论。

• 若第 $r$ 行在插入之前没有节点，则直接将 $first_r$ 指向节点 $id$。$id$ 的左、右指针均为本身，即 $id$。
• 若第 $r$ 行在插入之前有节点，则将节点 $id$ 插入到 $first_r$ 之后。

示例程序：

void insert(int r,int c){
    id++;//注意要改变下一次插入元素的编号
    row[id] = r,col[id] = c;
    sz[c]++;//这里需要增加行元素个数
    U[id] = c;
    D[id] = D[c];
    U[D[c]] = id;
    D[c] = id;
    if(!first[r]){
        first[r] = L[id] = R[id] = id;
    }
    else{
        L[id] = first[r];
        R[id] = R[first[r]];
        L[R[first[r]]] = id;
        R[first[r]] = id;
    }
}

dance 操作

dance(x) 操作能递归实现 X 算法，这个操作也是 DLX 算法的主体。

步骤如下：

1. 若 $0$ 号节点没有右节点，即矩阵（双十字链表）中没有任何元素时，算法结束，答案为 $S$ 中的所有元素。
2. 枚举所有列，找到 $sz$ 最小的列，即 $1$ 个数最少的列（这里与上文介绍 X 算法流程的部分有不同，这是为了使程序有启发性，使递归次数更少，也就是速度更快），使用 remove 操作删除它。
3. 枚举该列所有有 $1$ 的行，枚举其是否被选择。
4. 递归下去，如果找到答案，返回；如果无解，返回并报告无解；否则恢复该列。

示例程序：

bool dance(int x){
    if(!R[0]){
        ans = x;
        return 1;
    }
    int y = R[0];
    for(int i=R[0];i;i=R[i]){
        if(sz[i]<sz[y]){
            y = i;
        }
    }
    remove(y);
    for(int i=D[y];i!=y;i=D[i]){
        s[x] = row[i];
        for(int j=R[i];j!=i;j=R[j]){
            remove(col[j]);
        }
        if(dance(x+1)){
            return 1;
        }
        for(int j=L[i];j!=i;j=L[j]){
            recover(col[j]);
        }
    }
    recover(y);
}

最终程序/DLX 模板

struct DLX{
    int n,m,id,ans;
    int L[1005],R[1005],U[1005],D[1005],first[1005],sz[1005],row[1005],col[1005],s[1005];
    void build(int r,int c){
        n = r,m = c;
        for(int i=0;i<=m;i++){
            L[i] = i-1,R[i] = i+1;
            U[i] = i,D[i] = i;
        }
        L[0] = c;
        R[c] = 0;
        id = c+1;
    }
    void remove(int x){
        R[L[x]] = R[x];
        L[R[x]] = L[x];
        for(int y=U[x];y!=x;y=U[y]){
            for(int z=R[y];z!=y;z=R[z]){
                U[D[z]] = U[z];
                D[U[z]] = D[z];
                sz[col[z]]--;
            }
        }
    }
    void recover(int x){
        for(int y=U[x];y!=x;y=U[y]){
            for(int z=R[y];z!=y;z=R[z]){
                U[D[z]] = z;
                D[U[z]] = z;
                sz[col[z]]++;
            }
        }
        R[L[x]] = x;
        L[R[x]] = x;
    }
    void insert(int r,int c){
        row[id] = r,col[id] = c;
        sz[c]++;
        U[id] = c;
        D[id] = D[c];
        U[D[c]] = id;
        D[c] = id;
        if(!first[r]){
            first[r] = L[id] = R[id] = id;
        }
        else{
            L[id] = first[r];
            R[id] = R[first[r]];
            L[R[first[r]]] = id;
            R[first[r]] = id;
        }
        id++;
    }
    bool dance(int x){
        if(!R[0]){
            ans = x;
            return 1;
        }
        int y = R[0];
        for(int i=R[0];i;i=R[i]){
            if(sz[i]<sz[y]){
                y = i;
            }
        }
        remove(y);
        for(int i=D[y];i!=y;i=D[i]){
            s[x] = row[i];
            for(int j=R[i];j!=i;j=R[j]){
                remove(col[j]);
            }
            if(dance(x+1)){
                return 1;
            }
            for(int j=L[i];j!=i;j=L[j]){
                recover(col[j]);
            }
        }
        recover(y);
    }
}DancingLinks;

建模

基本思想

对于每道题，我们考虑行和列代表的意义。

行代表 决策，也就是选\不选。

列代表 状态，也就是约束条件。

对于某一行而言，由于不同的列的值不相同，我们 由不同的状态，定义了一个决策。

使用DLX数独问题

决策-行

依照上文，因为有 $9$ 行 $9$ 列，每个格子可以填的数组有 $[1,9]$（离散状态下），因此DLX有 $9^3$ 行，即 $729$ 行。

约束条件-列

在数独中，每填一个数可以使用三元组 $(x,y,z)$ 表示，即在第 $x$ 行，第 $y$ 列填入了数 $z$。

因此决策状态 $(x,y,z)$ 所造成的影响为：

• 第 $x$ 行使用了数 $z$，这一行不能继续使用该数。
• 第 $y$ 列使用了数 $z$，这一列不能继续使用该数。
• 设第 $x$ 行第 $y$ 列所在的宫为第 $w$ 宫，则第 $w$ 宫使用了数 $z$，这一宫不能继续使用该数。
• 第 $x$ 行第 $y$ 列填入的数 $z$，这个位置不能再次填数。

因此决策有 $4$ 种影响，数独里有 $81$ 个格子，因此有 $81 \times 4$ 列，即 $324$ 列。有 $729 \times 4$ 即 $2916$ 个 $1$。

由于这一部分较难理解，同时较难说明，因此标程中不予注释。

标程

9×9 大小

例题：UVA1309

#include<bits/stdc++.h>
using namespace std;
int a[105][105];
struct DLX{
    int n,m,id,ans;
    int L[200005],R[200005],U[200005],D[200005],first[200005],sz[200005],row[200005],col[200005],s[200005];
    void build(int r,int c){
        memset(L,0,sizeof(L));
        memset(R,0,sizeof(R));
        memset(U,0,sizeof(U));
        memset(R,0,sizeof(R));
        memset(first,0,sizeof(first));
        memset(sz,0,sizeof(sz));
        memset(row,0,sizeof(row));
        memset(col,0,sizeof(col));
        memset(s,0,sizeof(s));
        n = r,m = c;
        for(int i=0;i<=m;i++){
            L[i] = i-1,R[i] = i+1;
            U[i] = i,D[i] = i;
        }
        L[0] = c;
        R[c] = 0;
        id = c+1;
    }
    void remove(int x){
        R[L[x]] = R[x];
        L[R[x]] = L[x];
        for(int i=D[x];i!=x;i=D[i]){
            for(int j=R[i];j!=i;j=R[j]){
                sz[col[j]]--;
                U[D[j]] = U[j];
                D[U[j]] = D[j];
            }
        }
    }
    void recover(int x){
        for(int i=U[x];i!=x;i=U[i]){
            for(int j=L[i];j!=i;j=L[j]){
                D[U[j]] = U[D[j]] = j;
                sz[col[j]]++;
            }
        }
        R[L[x]] = L[R[x]] = x;
    }
    void insert(int r,int c){
        id++;
        row[id] = r,col[id] = c;
        sz[c]++;
        U[id] = c;
        D[id] = D[c];
        D[c] = U[D[c]] = id;
        if(!first[r]){
            first[r] = L[id] = R[id] = id;
        }
        else{
            L[id] = first[r];
            R[id] = R[first[r]];
            R[first[r]] = L[R[first[r]]] = id;
        }
    }
    bool dance(int x){
        if(!R[0]){
            for(int i=1;i<x;i++){
                a[(s[i]-1)/256+1][(s[i]-1)/16%16+1] = (s[i]-1)%16+1;
            }
            return 1;
        }
        int y = R[0];
        for(int i=R[0];i;i=R[i]){
            if(sz[i]<sz[y]){
                y = i;
            }
        }
        remove(y);
        for(int i=D[y];i!=y;i=D[i]){
            s[x] = row[i];
            for(int j=R[i];j!=i;j=R[j]){
                remove(col[j]);
            }
            if(dance(x+1)){
                return 1;
            }
            for(int j=L[i];j!=i;j=L[j]){
                recover(col[j]);
            }
        }
        recover(y);
        return 0;
    }
}DancingLinks;
void work(int x,int y,int z){
    int idx = (x-1)*256+(y-1)*16+z;
    DancingLinks.insert(idx,(x-1)*16+z);
    DancingLinks.insert(idx,(y-1)*16+z+256);
    DancingLinks.insert(idx,((x-1)/4*4+(y-1)/4)*16+z+512);
    DancingLinks.insert(idx,(x-1)*16+y+768);
}
int main(){
    string s;
    int cnt = 0;
    while(cin >> s){
        cnt++;
        if(cnt>1){
            cout << endl;
        }
        DancingLinks.build(4096,1024);
        for(int i=1;i<=16;i++){
            if(i!=1){
                cin >> s;
            }
            for(int j=1;j<=16;j++){
                char c = s[j-1];
                if(c!='-'){
                    a[i][j] = c-'A'+1;
                    work(i,j,a[i][j]);
                }
                else{
                    for(int k=1;k<=16;k++){
                        work(i,j,k);
                    }
                }
            }
        }
        DancingLinks.dance(1);
        for(int i=1;i<=16;i++){
            for(int j=1;j<=16;j++){
                cout << (char)(a[i][j]+'A'-1);
            }
            cout << endl;
        }
    }
    return 0;
}

16×16 大小

例题：UVA1309

基本思路与上文一致，仅需将计算行、列、宫时的公式换成 $16 \times 16$ 大小的公式，再将数组空间开大即可。

#include<bits/stdc++.h>
using namespace std;
int a[105][105];
struct DLX{
    int n,m,id,ans;
    int L[200005],R[200005],U[200005],D[200005],first[200005],sz[200005],row[200005],col[200005],s[200005];
    void build(int r,int c){
        memset(L,0,sizeof(L));
        memset(R,0,sizeof(R));
        memset(U,0,sizeof(U));
        memset(R,0,sizeof(R));
        memset(first,0,sizeof(first));
        memset(sz,0,sizeof(sz));
        memset(row,0,sizeof(row));
        memset(col,0,sizeof(col));
        memset(s,0,sizeof(s));
        n = r,m = c;
        for(int i=0;i<=m;i++){
            L[i] = i-1,R[i] = i+1;
            U[i] = i,D[i] = i;
        }
        L[0] = c;
        R[c] = 0;
        id = c+1;
    }
    void remove(int x){
        R[L[x]] = R[x];
        L[R[x]] = L[x];
        for(int i=D[x];i!=x;i=D[i]){
            for(int j=R[i];j!=i;j=R[j]){
                sz[col[j]]--;
                U[D[j]] = U[j];
                D[U[j]] = D[j];
            }
        }
    }
    void recover(int x){
        for(int i=U[x];i!=x;i=U[i]){
            for(int j=L[i];j!=i;j=L[j]){
                D[U[j]] = U[D[j]] = j;
                sz[col[j]]++;
            }
        }
        R[L[x]] = L[R[x]] = x;
    }
    void insert(int r,int c){
        id++;
        row[id] = r,col[id] = c;
        sz[c]++;
        U[id] = c;
        D[id] = D[c];
        D[c] = U[D[c]] = id;
        if(!first[r]){
            first[r] = L[id] = R[id] = id;
        }
        else{
            L[id] = first[r];
            R[id] = R[first[r]];
            R[first[r]] = L[R[first[r]]] = id;
        }
    }
    bool dance(int x){
        if(!R[0]){
            for(int i=1;i<x;i++){
                a[(s[i]-1)/256+1][(s[i]-1)/16%16+1] = (s[i]-1)%16+1;
            }
            return 1;
        }
        int y = R[0];
        for(int i=R[0];i;i=R[i]){
            if(sz[i]<sz[y]){
                y = i;
            }
        }
        remove(y);
        for(int i=D[y];i!=y;i=D[i]){
            s[x] = row[i];
            for(int j=R[i];j!=i;j=R[j]){
                remove(col[j]);
            }
            if(dance(x+1)){
                return 1;
            }
            for(int j=L[i];j!=i;j=L[j]){
                recover(col[j]);
            }
        }
        recover(y);
        return 0;
    }
}DancingLinks;
void work(int x,int y,int z){
    int idx = (x-1)*256+(y-1)*16+z;
    DancingLinks.insert(idx,(x-1)*16+z);
    DancingLinks.insert(idx,(y-1)*16+z+256);
    DancingLinks.insert(idx,((x-1)/4*4+(y-1)/4)*16+z+512);
    DancingLinks.insert(idx,(x-1)*16+y+768);
}
int main(){
    string s;
    int cnt = 0;
    while(cin >> s){
        cnt++;
        if(cnt>1){
            cout << endl;
        }
        DancingLinks.build(4096,1024);
        for(int i=1;i<=16;i++){
            if(i!=1){
                cin >> s;
            }
            for(int j=1;j<=16;j++){
                char c = s[j-1];
                if(c!='-'){
                    a[i][j] = c-'A'+1;
                    work(i,j,a[i][j]);
                }
                else{
                    for(int k=1;k<=16;k++){
                        work(i,j,k);
                    }
                }
            }
        }
        DancingLinks.dance(1);
        for(int i=1;i<=16;i++){
            for(int j=1;j<=16;j++){
                cout << (char)(a[i][j]+'A'-1);
            }
            cout << endl;
        }
    }
    return 0;
}