一.总体思路

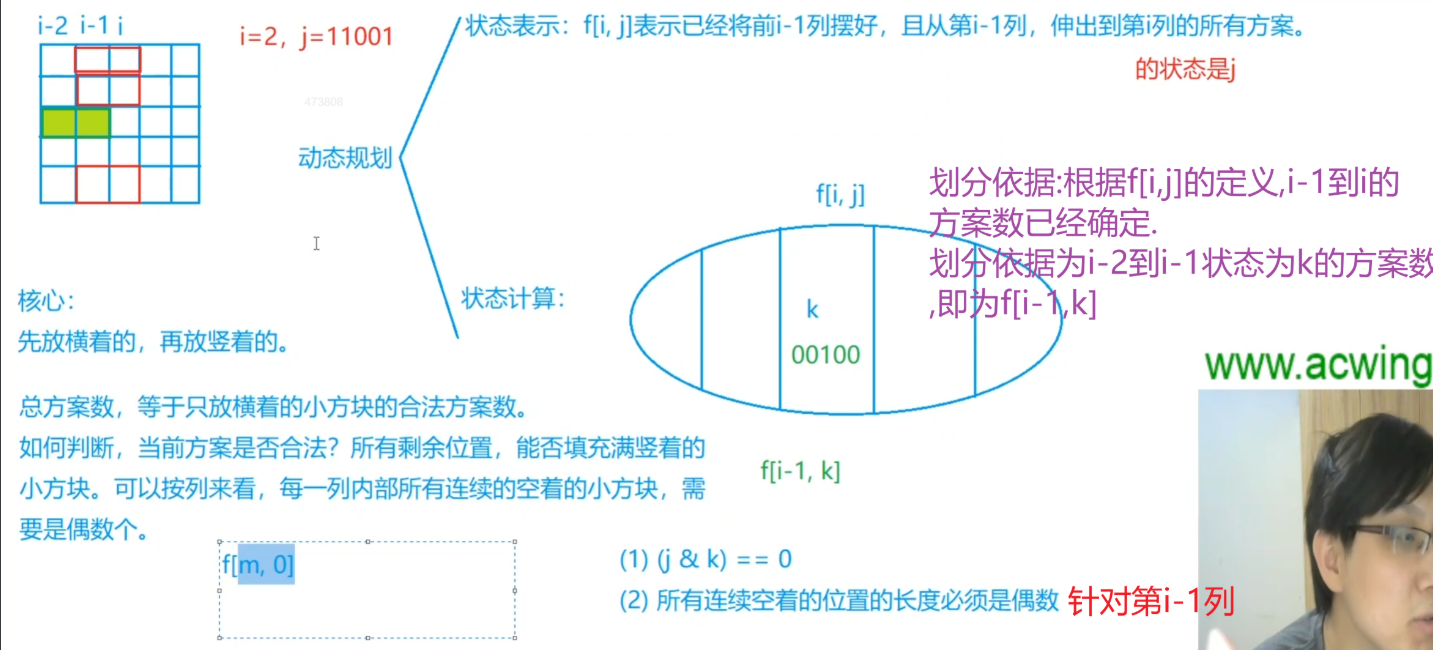
本题关键:当横向摆放的方式确定以后,竖着摆放的方式就只有一种了,
所以横着摆放的方式即为所有方块摆放的方式

f[i,j]表示的意义:前i-1列已经排好,且第i-1伸向第i列的状态j的方案数

划分依据:已知i-1列到i列的状态j的方案数,和之前y总讲的大部分DP问题
相似,以最后一次为突破口.将集合以i-2到i-1的状态k进行划分.
即f[i-1,k],如果f[i-1,k]与f[i,j]不冲突,则f[i,j] = f[i,j]+f[i-1,k];
以二进制的方法划分,最多可以划分为2^n种,n为行数

对于f[i,j] = f[i,j]+f[i-1,k]的理解
只要有符合i-2列到i-1列,且不破坏f[i][j]与f[i-1][k]的合法性的方案就累加起来

二.代码部分
2.1 预处理

1<[HTML_REMOVED]>N同理,即为除以N个2

预处理目的:将指定的方格中合法的状态保留,以节省后续时间

关键
(i>>j &1)==1
意义:状态i的第j位是否为1

(cnt&1)==1
意义:遇到1之前连续的0的个数是否为奇数

若满足上述两种情况,举例:i = 0100
这里因为我们的前提是横着摆,且给每列留出的连续的空必须是偶数个
这样一来,i便不合法,所以状态i为false

2.2 判断第i列与i-1列是否可以联合
关键
(i&j)==0 && st[i | j]
i-1列与i列不重叠 且 i列和j列合并后,连续的0的个数为偶数个

2.3 DP部分
遍历1-m列,看第i-1列的状态与第i列的状态是否可以联合
可以联合即让方案数+f[i-1][k]

import java.util.*;
public class Main{
    public static void main(String[] args){
        /**
         * f[i][j] 表示前i-1列排好,且第i-1列伸向第i列的状态为j(二进制数)的方案数
         * state[j][k] 表示第i-1列 状态j 和第i列 状态k 是否可以联合
         * st[i] 表是每一种 列状态i是否合法
         **/ 
        Scanner sc = new Scanner(System.in);
        int N =12,M = 1<<N;// M = 2^N
        long[][]f = new long[N][M];
        int [][]state = new int[M][M];
        boolean[]st = new boolean[M];


        while(true){
            int n = sc.nextInt();
            int m = sc.nextInt();
            if(n == 0 && m == 0){ // 如果n跟m同时为0结束循环
                break;
            }

            /**
             * 预处理:
             * 遍历每一种状态i,st[i]表示i状态在当前n*m的方格内是否合法
             * 
             * 目的:
             * 去除不合法的状态,节省时间
             * 
             * cnt表示遇到1之前,前面连续的0的个数
             * 每一次遇到1之后就被重置为0
             * 例00100010
             * 第一个1前面连续的0的个数为2个
             * 第二个1前面连续的0的个数为3个
             * 
             * j表示行数索引,即当前状态i的第几行
             * 
             * 如何判断每个状态是否合法:
             * 如果有奇数个连续的0即为不合法
             **/ 
            for(int i = 0;i < 1<<n; i++){
                int cnt = 0;
                boolean flag = true;
                for(int j = 0; j < n;j++){
                    if((i>>j &1)==1){
                        if((cnt&1)==1){
                            flag = false;
                            break;
                        }
                        cnt = 0;
                    }else cnt++;
                }
                if((cnt&1)==1) flag = false;
                st[i] = flag;
            }

            /**
             * 对于符号 & 和 | 的理解
             * &相当于交集 011 & 010 = 010
             * |相当与并集 011 | 010 = 011
             **/ 
            /**
             * 查看第i-1列和第i列是否可以合并
             * 
             * i表示第i列的状态
             * j表示第i-1列的状态
             * 
             * i&j:检测两列是否有重叠
             * st[i|j]:表示两列合并的状态在方格中是否合法
             * i|j会把两列中都是0的行保存为0
             * 例:i:0011
             *    j:0101
             *  i|j:0111 这种即为非法
             * 
             * state[i][j] = 1表示i-1列和i列可以联合
             **/ 
            for(int i = 0;i<1<<n;i++){
                Arrays.fill(state[i],0);
                for(int j = 0;j<1<<n;j++){
                    if((i&j)==0 && st[i | j]){
                        state[i][j] = 1;
                    }
                }
            }

            //将所有方案初始化为0          
            for(int i = 0 ; i < N ; i ++ )
                Arrays.fill(f[i],0);
            f[0][0] = 1;// -1列不存在,不能伸到第0列,所以-1列状态为 000000...,方案数为1 


            /**
             * DP部分:
             * 当状态j和状态k可以联合时,那么方案数就累加
             **/ 
            for(int i = 1 ; i <= m ; i ++ ){ 
                //枚举i - 1 到 i的所有方案
                for(int j = 0 ; j < 1 << n ; j ++ ){
                    //枚举i - 2 到 i - 1 的所有方案
                    for(int k = 0 ; k < 1 << n ; k ++ ){
                        //现在的方案等于前面每种k方案的总和
                        if(state[j][k] == 1) f[i][j] += f[i - 1][k];
                    }
                }
            }
            System.out.println(f[m][0]);
        }
    }
}