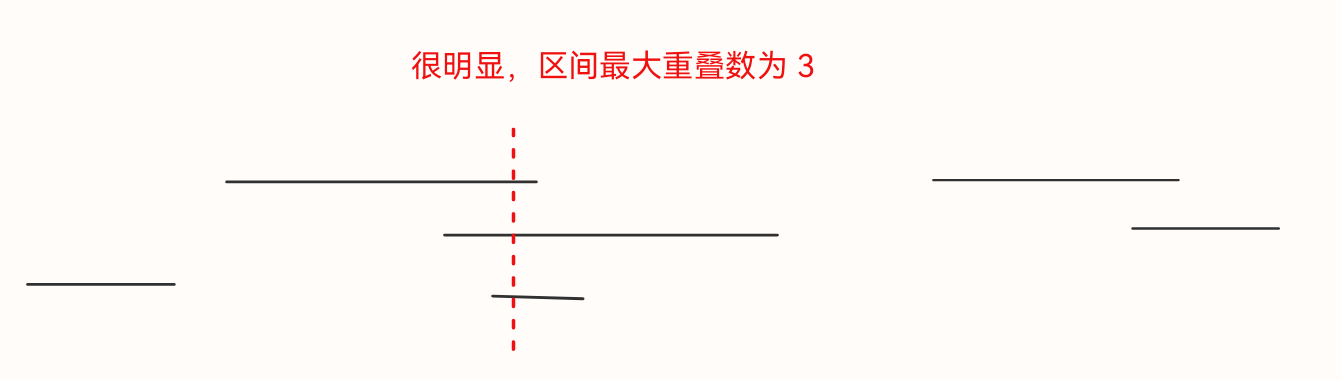
本题也可以叫做区间最大重叠数

从上方往下做垂线，与区间的交点个数最多的数

本题的输入样例：

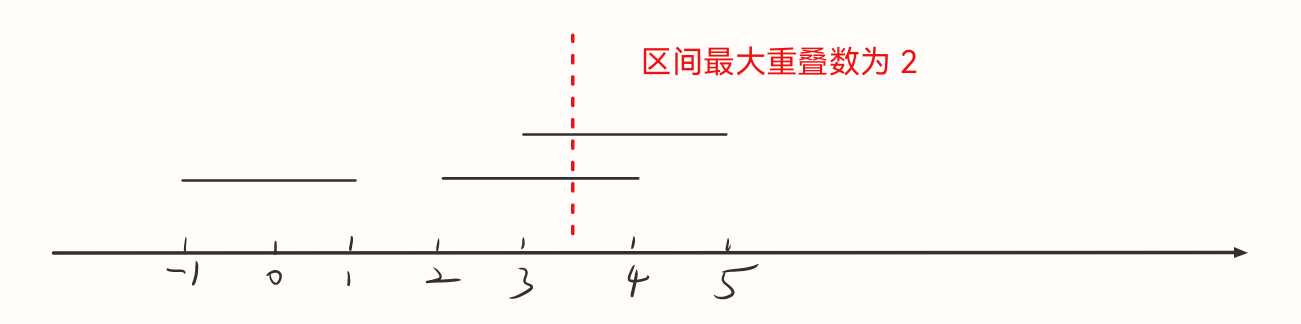
因此本题就可以转化为区间求和问题：体现为统计每个点的频率，读入每个区间[l,r]，将数组a[l] ~ a[r]的每一个数都加上1，直到读完所有的区间为止。然后统计数组a[]的最大值就是答案了。

但是本题的输入数据中区间的范围为$[-10^9,10^9]$，很明显不能直接开那么大的数组，否则肯定MLE。注意观察到本题实际要用到的数据最多只有$2 \times 10^5$，因此可以用离散化来解这道题，并且这题是有序离散化。

此外，区间求和用差分做可以做到$O(1)$的时间复杂度，所以本题的时间复杂度瓶颈就是排序了，即$O(nlogn)$

#include <iostream>
#include <vector>
#include <unordered_map>
#include <algorithm>
#include <set>
using namespace std;

const int N = 2e5 + 10;

typedef pair<int,int> PII;

unordered_map<int,int> discrete; // 离散化存反映射用的

// a为存数据的数组，b为其差分数组
int a[N],b[N];

// set实现排序去重
set<int> alls; // 存放所有要用到的下标

/*
存放所有的区间
因为必须要把所有要用到的下标都读入后才能做离散化，进而才能去做操作
*/
vector<PII> range;

int n;

int main(){
    scanf("%d",&n);
    for(int i = 0;i < n;i ++){
        int l,r;
        scanf("%d%d",&l,&r);
        alls.insert(l);
        alls.insert(r);
        range.push_back({l,r});
    }
    // 此时所有要用到的区间的点都已经读入了，并且已经排序去重了
    // 存反映射，因为要使用前缀和，差分数组，所以下标要从1开始
    int cnt = 1;
    for(auto x : alls){
        discrete[x] = cnt ++;
    }
    for(int i = 1;i < cnt;i ++){
        b[i] = a[i] - a[i - 1]; // 初始化差分数组
    }

    for(int i = 0;i < range.size();i ++){
        int l = range[i].first; // l为没有离散化之前的下标
        int r = range[i].second; // r为没有离散化之前的下标
        int discrete_l = discrete[l]; // discrete_l为l离散化之后的下标
        int discrete_r = discrete[r]; // discrete_r为r离散化之后的下标
        b[discrete_l] ++,b[discrete_r + 1] --; // [discrete_l,discrete_r]区间的数加上1
    }
    int ans = 0;
    for(int i = 1;i < cnt;i ++){
        a[i] = a[i - 1] + b[i]; // 由差分数组得到原数组
        ans = max(ans,a[i]); // 记录频率最大值
    }
    cout << ans;
    return 0;
}