题目描述

在一棵无限的二叉树上，每个节点都有两个子结点，树中的结点逐行依次进行标记。

如下图所示，在奇数行（即，第一行、第三行、第五行……）中，按从左到右的顺序进行标记；

而偶数行（即，第二行、第四行、第六行……）中，按从右到左的顺序进行标记。

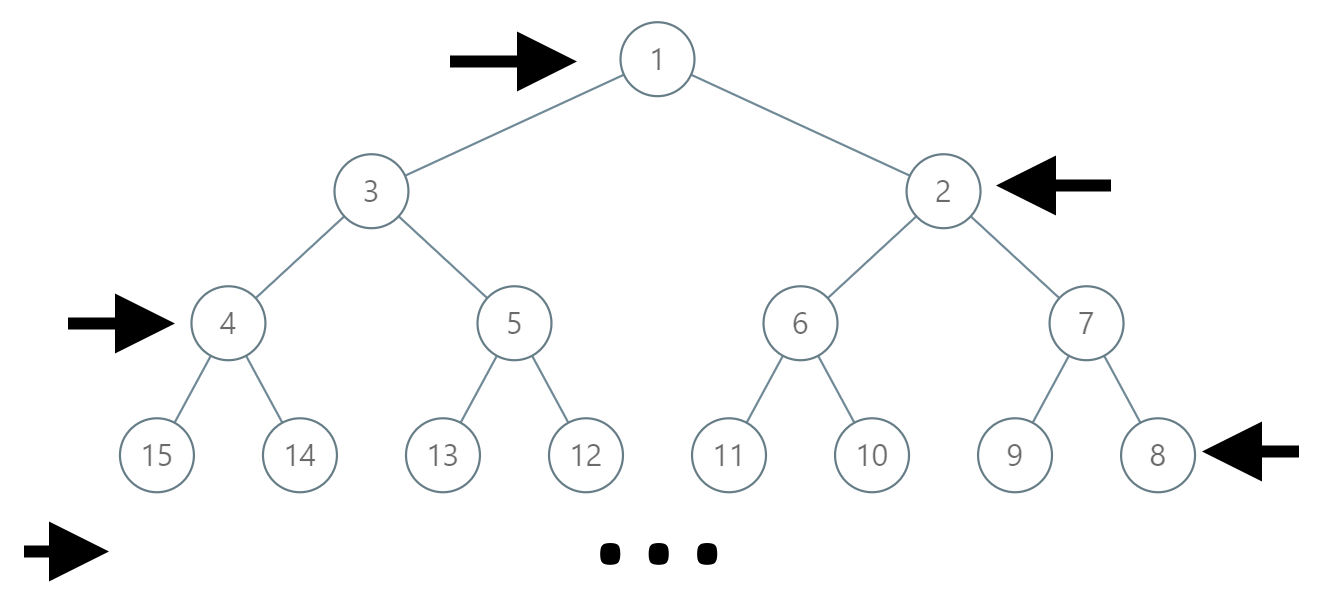
给你树上某一个节点的标号 label，请你返回从根节点到该标号为 label 结点的路径，该路径是由途经的结点标号所组成的。

样例

输入：label = 14
输出：[1,3,4,14]

输入：label = 26
输出：[1,2,6,10,26]

限制

• 1 <= label <= 10^6

算法

(找规律) $O(\log n)$

1. 由于二叉树每层结点个数增加的都是 2 的幂次，可以感觉到这和位运算有关系。
2. 进一步发现，如果确定了某一层结点的相对位置，则相对位置除以 2，就是上一层的相对位置。这里的相对位置指的是距离当前层最左结点的距离。
3. 所以我们可以求出每一层的相对位置，根据相对位置，恢复标号值，这里的标号值都是按照正常从左到右的顺序编号。
4. 以 14 为例，14 的二进制表示为 1110，如果是正常每次都从左到右标号，则 14 的相对位置应该是 110；但此题是之字形标号，则相对位置为 1111 - 1110 = 1，传播到上一层的相对位置就是 1 >> 1 = 0，则上一层的标号就是 100 + 0 = 100。
5. 看到这里有些读者会发现，14 恰好在第四行，如果一开始不是在偶数行怎么办？这里其实不用担心奇数和偶数行，因为初始时是从右向左还是从左向右不会影响答案。所以，我们初始时可以假设是从右向左的标号，求出距离当前层最右结点的相对位置，传播到上一层，然后获取上一层距离最左结点相对位置的标号值。下面会分别模拟 14 和 26 两种情况的例子。
6. 对于 14 的完整过程如下：
   1. 1110，初始标号值为 14。
   2. 1111 - 1110 = 001, 001 >> 1 = 00, 100 + 00 = 100，上一层的标号值为 4。
   3. 111 - 100 = 11, 11 >> 1 = 1, 10 + 1 = 11，再上一层的标号值 3。
   4. 11 - 11 = 0, 0 >> 1 = 0, 1 + 0 = 1，到达最顶层 1。
7. 对于 26 的完整过程如下：
   1. 11010，初始标号值为 26。
   2. 11111 - 11010 = 0101, 0101 >> 1 = 010, 1000 + 010 = 1010，上一层的标号值为 10。
   3. 1111 - 1010 = 101, 101 >> 1 = 10, 100 + 10 = 110，标号值为 6。
   4. 111 - 110 = 01, 01 >> 1 = 0, 10 + 0 = 10，标号值为 2。
   5. 11 - 10 = 1, 1 >> 1 = 0, 1 + 0 = 1，到达最顶层 1。

时间复杂度

• 循环最多与 $n$ 的二进制位数有关，故时间复杂度为 $O(\log n)$。

空间复杂度

• 存储答案需要 $O(\log n)$ 的空间。

C++ 代码

class Solution {
public:
    vector<int> pathInZigZagTree(int label) {
        vector<int> ans;

        int h = 0;
        while ((label >> (h + 1)) > 0)
            h++;

        ans.push_back(label);
        while (h > 0) {
            int pos = ((1 << (h + 1)) - 1 - label) >> 1;
            label = (1 << (h - 1)) + pos;
            h--;
            ans.push_back(label);
        }

        reverse(ans.begin(), ans.end());

        return ans;
    }
};