题目描述

给出二叉树的根节点 root，树上每个节点都有一个不同的值。

如果节点值在 to_delete 中出现，我们就把该节点从树上删去，最后得到一个森林（一些不相交的树构成的集合）。

返回森林中的每棵树。你可以按任意顺序组织答案。

样例

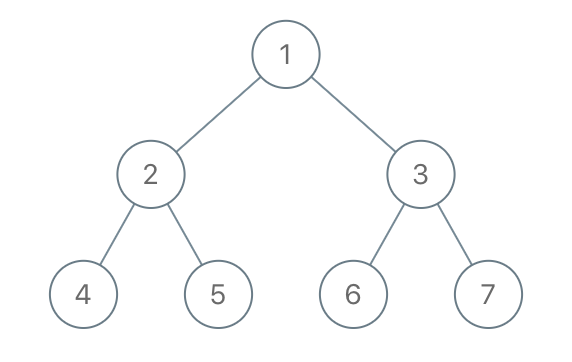
输入：root = [1,2,3,4,5,6,7], to_delete = [3,5]
输出：[[1,2,null,4],[6],[7]]

限制

• 树中的节点数最大为 1000。
• 每个节点都有一个介于 1 到 1000 之间的值，且各不相同。
• to_delete.length <= 1000
• to_delete 包含从 1 到 1000 各不相同的值。

算法

(递归) $O(n)$

1. 定义递归函数 solve，包含参数为当前结点的引用 r，是否要被添加到答案数组中 add_to_ans。我们在主函数中调用 solve，传递整棵树的根结点作为当前结点，且 add_to_ans=true 。
2. 如果当前结点为空，则直接返回。
3. 如果当前结点在 to_delete 中出现过，则分别递归左右子结点，递归的 add_to_ans=true，然后当前结点变成 NULL。
4. 否则，分别递归左右子结点，递归的 add_to_ans=false。如果当前层的 add_to_ans 为 true，则将当前结点 r 加入到数组中。

时间复杂度

• 每个结点仅遍历一次，检查是否在 to_delete 中出现过为常数的时间复杂度，故总时间复杂度为 $O(n)$。

空间复杂度

• 需要额外的哈希表存储 to_delete，递归需要系统栈空间，故总空间复杂度为 $O(n)$。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    void solve(TreeNode* &r, bool add_to_ans,
               vector<TreeNode*>& ans,
               const unordered_set<int>& to_del) {
        if (r == NULL)
            return;

        if (to_del.find(r -> val) != to_del.end()) {
            solve(r -> left, true, ans, to_del);
            solve(r -> right, true, ans, to_del);
            r = NULL;
        } else {
            solve(r -> left, false, ans, to_del);
            solve(r -> right, false, ans, to_del);
            if (add_to_ans)
                ans.push_back(r);
        }
    }

    vector<TreeNode*> delNodes(TreeNode* root, vector<int>& to_delete) {
        vector<TreeNode*> ans;
        unordered_set<int> to_del(to_delete.begin(), to_delete.end());
        solve(root, true, ans, to_del);
        return ans;
    }
};