历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

AcWing 340. 通信线路原题链接中等

作者：

銘权 , 2019-07-11 14:29:30 , 所有人可见 , 阅读 13035

108

46

题目描述

N 个点，P 条边，求 1 到 N 的最小花费，如果经过的边数小于 K ，花费为 0 ，否则花费为 K+1 大的边权值

样例

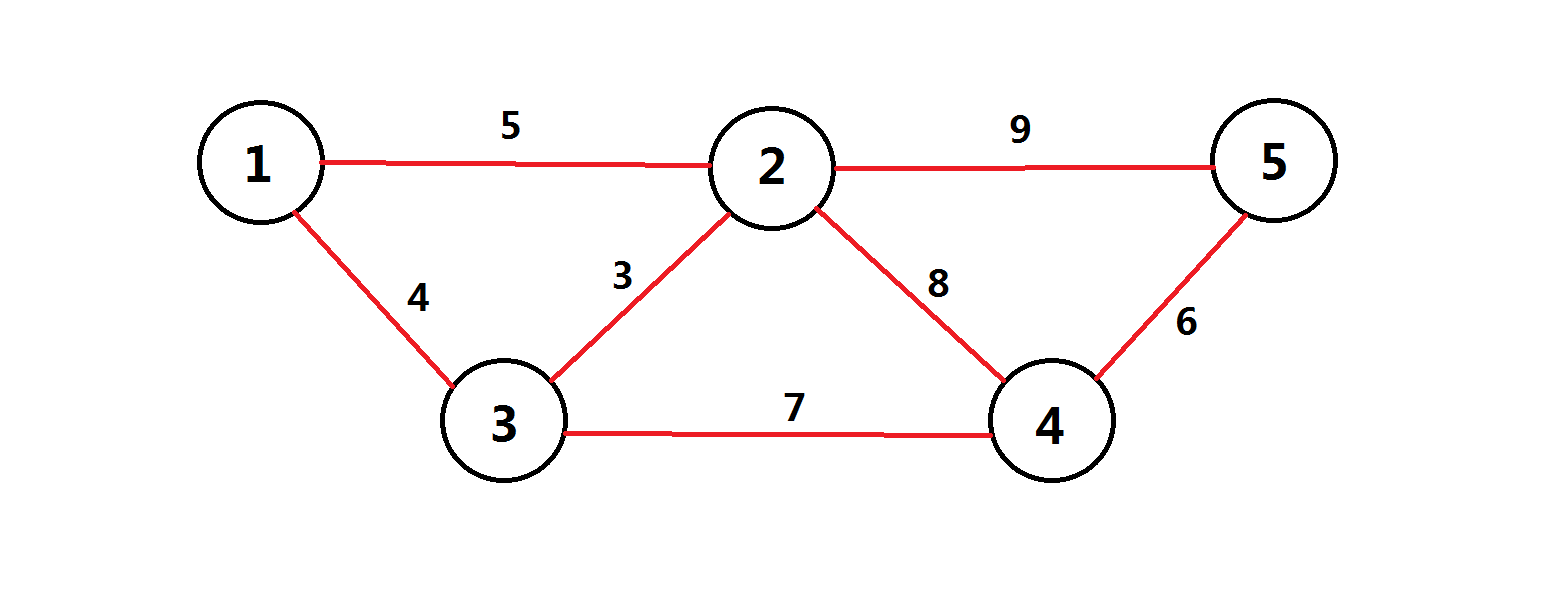
``` 电话线1.png

分层图最短路

什么是分层图：

当同一个点可以有不同的操作时，我们将一个点分开，对应不同的操作，再重新与其他点相连
我们对每个点都进行如此操作后，原本只有一层的图就被我们分层了
我们把样例分层，如图：

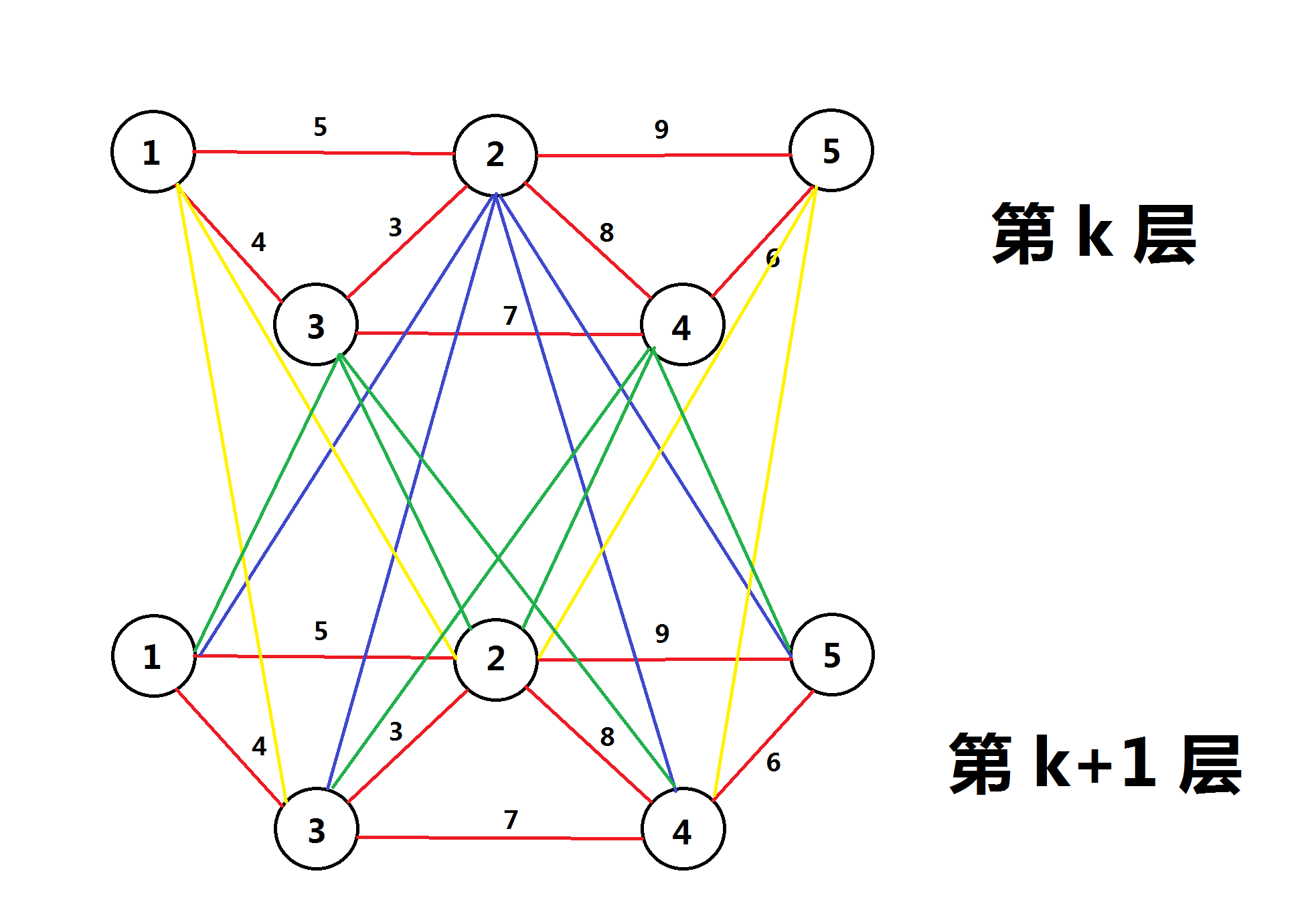
``` 电话线2.png

红边是普通边，其他颜色的边是进行免费操作的边

分层图的作用


经过分层后，我们得到了新图
我们可以发现，原本题目中选 k 条边免费的操作被我们等价了：
在从一个点到另一个点时，如果选择免费，就进入下一层，相当于进行一次免费操作

因为可以免费 k 次，所以我们要建 k+1 层图

在 k+1 层图上我们已经不能再往下了，即免费操作已用完

那么，如何建边呢？

代码实现：


    for(int i=1,x,y,z;i<=p;i++)
    {
        scanf("%d%d%d",&x,&y,&z);
        add(x,y,z);
        add(y,x,z);    //本层建边
        for(int j=1,z1=0;j<=k;j++)
        {
            add(x+(j-1)*n,y+j*n,z1);    //第j层和第j+1层间的建边
            add(y+(j-1)*n,x+j*n,z1);
            add(x+j*n,y+j*n,z);
            add(y+j*n,x+j*n,z);    //第j+1层建边
        }
    }

关于本题

那么，本题已经很明显可以用分层图做

但是

由于最终花费是权值最大的边
所以，在更新最短路的操作中，需要略微变动
以前我们是这么更新的：

if ( dis[y] > dis[x] + z ) dis[y] = dis[x] + z;

现在我们要这么更新：

z=max(edge,dis[x]); //edge是当前边权值

if ( dis[y] > z ) dis[y] = z;

AC代码

#include<bits/stdc++.h>
using namespace std;

const int N=1000000+10,M=10000000+10;

int n,p,k;
int tot=0;
priority_queue< pair<int ,int> > q;
struct node
{
    int ver,nex,edge;
}po[M];
int head[N],dis[N];
bool v[N];

void add(int x,int y,int z)
{
    po[++tot].ver=y,po[tot].edge=z;
    po[tot].nex=head[x],head[x]=tot;
}

void dijkstra()
{
    memset(dis,0x3f,sizeof(dis));
    dis[1]=0;
    q.push(make_pair(0,1));
    while(q.size())
    {
        int x=q.top().second;
        q.pop();
        if(v[x]) continue;
        v[x]=true;
        for(int i=head[x];i;i=po[i].nex)
        {
            int y=po[i].ver,z=max(po[i].edge,dis[x]);
            if(dis[y]>z)
            {
                dis[y]=z;
                q.push(make_pair(-dis[y],y));
            }
        }
    }
}

int main()
{
    scanf("%d%d%d",&n,&p,&k);
    for(int i=1,x,y,z;i<=p;i++)
    {
        scanf("%d%d%d",&x,&y,&z);
        add(x,y,z);
        add(y,x,z);
        for(int j=1,z1=0;j<=k;j++)
        {
            add(x+(j-1)*n,y+j*n,z1);
            add(y+(j-1)*n,x+j*n,z1);
            add(x+j*n,y+j*n,z);
            add(y+j*n,x+j*n,z);
        }
    }
    for(int i=1,z=0;i<=k;i++)
        add(i*n,(i+1)*n,z);
    //如果读者认真观察代码的话一定会问为什么要有如此操作
    //那么读者仔细思考，若无此操作，如果有一组数据 1 到 N 经过的边小于 k ，会发生什么呢？

    dijkstra();

    if(dis[(k+1)*n]==1061109567) puts("-1");
    else printf("%d",dis[(k+1)*n]);
    //感谢 Schelski 指出的错误：忘记判路径是否存在了。。。
    return 0;
}

62 评论

drizzy 2022-07-25 16:37

贴个spfa的做法

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
typedef pair<int, int> PII;
const int INF = 0x3f3f3f3f;
const int N = 1010, M = 20010, K = 1010;

int n, m, k;
int h[N], w[M], e[M], ne[M], idx;
int dist[N][K];  //dist[x][k]表示从1到达x节点，途中使用k次免费升级的最小花费
bool vis[N][K];

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

int spfa() {
    memset(dist, 0x3f, sizeof dist);
    dist[1][0] = 0;
    queue<PII> q;
    q.emplace(1, 0);
    vis[1][0] = true;

    while (!q.empty()) {
        auto [v, cnt] = q.front();
        q.pop();

        vis[v][cnt] = false;

        for (int i = h[v]; ~i; i = ne[i]) {
            int j = e[i];
            if (cnt < k && dist[j][cnt + 1] > dist[v][cnt]) {  //使用一次免费升级
                dist[j][cnt + 1] = dist[v][cnt];
                if (!vis[j][cnt + 1]) {
                    q.emplace(j, cnt + 1);
                    vis[j][cnt + 1] = true;
                }
            }
            if (dist[j][cnt] > max(w[i], dist[v][cnt])) {  //不使用免费升级
                dist[j][cnt] = max(w[i], dist[v][cnt]);
                if (!vis[j][cnt]) {
                    q.emplace(j, cnt);
                    vis[j][cnt] = true;
                }
            }
        }
    }

    int res = INF;
    for (int i = 0; i <= k; i++) {
        res = min(res, dist[n][i]);
    }
    return res == INF ? -1 : res;
}

int main() {
    scanf("%d%d%d", &n, &m, &k);

    memset(h, -1, sizeof h);
    while (m--) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c), add(b, a, c);
    }

    cout << spfa() << endl;

    return 0;
}

smile是对你的礼貌 2023-09-11 20:40

后效性怎么解决的啊？想不通

Mr.青苹果 2023-03-26 16:44

int y=po[i].ver,z=max(po[i].edge,dis[x]);
if(dis[y]>z)
{
dis[y]=z;
q.push(make_pair(-dis[y],y));
}
能仔细讲一下这段代码吗，实在是看不懂....

ttdykdy 2个月前

代码中优先队列是大根堆，所以存负值

whsstory 2019-09-22 13:28

分层图最短路,是个不错的想法.但是像本题这样层数较多的话,其$O(mk)$的空间可能会被卡

銘权 2019-09-23 20:22

确实是这样，但我看到没人用这种写法，于是来一发
而且个人觉得这样写比较易懂
但主要是当时刚学分层图，遇到最短路题目就想用分层图解~哈哈

whsstory 2019-09-23 20:30 回复了銘权的评论

先Orz再说

whsstory 2019-09-23 20:31 回复了 whsstory 的评论

这句话应该没有歧义吧[汗]就是Orz您

糖豆 2022-10-24 11:20

直接k+1层建图可能会MLE，如果是多维数组的话，问题就不大了

bNd.top++ 6个月前

确实，要是严格按边数取值范围，设置上限1e7就会Memory Limit Exceeded

古河渚 3个月前

%%%

如鲸向海_3 6个月前

边权取反用大根堆等价于不取反用小根堆

shmily 2023-01-18 12:49

太妙了，tql

lovecan 2022-10-13 13:13

if(dis[y]>z)
{
dis[y]=z;
q.push(make_pair(-dis[y],y));
}

这是什么意思啊不是要取最大花费吗

mount_nianbao 2022-11-13 01:22

因为q是大根堆，要使dis[y]最小就是使-dis[y]最大

CHENL 2022-08-11 00:26

给每层终点建一条边是为了防止出现用不到k次就出现最短路的情况么,有点想不明白

ootori 2022-09-11 17:10

是这样的相当于到了就可以免费去最后一层

糖豆 2022-10-24 11:18

分层图的例题可以看一下我整理的题解：https://www.cnblogs.com/littlehb/p/16815959.html

253718226 10个月前回复了 ootori 的评论

终点是在最后一层，必须k次啊

zzuzhou 8个月前回复了糖豆的评论

写的很不错，受益匪浅！膜拜大佬，把你的链接收藏进我的笔记里面了，谢谢大佬！

WXY呀 2022-07-29 15:42

数据加强了吗？现在直接复制大佬的代码交都有一组过不了还有一个疑问 Dijkstra不是不可以处理负权边的吗？

Amazing32510 2022-07-31 11:42

这里放相反数是为了求最大吧

Amazing32510 2022-07-31 12:11 回复了 Amazing32510 的评论

https://blog.csdn.net/malimingwq/article/details/89436697?depth_1-utm_source=
这里有讲为啥不能处理负权边的

WXY呀 2022-08-01 11:09 回复了 Amazing32510 的评论

取反之后不就变负权了吗这题这种做法怎么都会错就是过不了我最后用的二分+spfa过的

Amazing32510 2022-08-01 11:50 回复了 WXY呀的评论

雀氏，二分+spfa简单点，我分层图还没学会（不知道为啥要建下一层到上层的反向边）

Amazing32510 2022-08-01 11:52 回复了 WXY呀的评论

但是不是所有的都变负权了么，那不就没关系了，dijstra应该是处理不了负环吧

WXY呀 2022-08-02 19:45 回复了 Amazing32510 的评论

下层到上层的边不用建从上层到下层就已经代表了做了一次选择如果还能回到上层的话会出问题的

Amazing32510 2022-08-02 20:03 回复了 WXY呀的评论

雀氏，我也觉得，但是他们题解都建了…比如他这上面的 add(y+(j-1)n,x+jn,z1);

WXY呀 2022-08-02 20:07 回复了 Amazing32510 的评论

emmm 很巧我有过和你一样的疑问看来大家的学习过程都差不多哈哈哈你可以把这些边都打印出来 debug看起来很麻烦当你打印出来的时候你这个疑问就会消除了因为这条边并不是前面那条边的反向边

Amazing32510 2022-08-03 08:12 回复了 WXY呀的评论

对哦雀氏不是反向边，hhh我悟了谢谢佬

WYCTSTF 2022-08-10 18:32 回复了 Amazing32510 的评论

不是负环，就是处理不了带负权的边，，取负放优先队列里只是一种技巧，省得写重载小于号而已

WYCTSTF 2022-08-10 18:33

数据还是挺弱的，分层图做法你可以看看我这个..
https://www.acwing.com/activity/content/code/content/3199369/

onepiece_ 2022-08-25 11:31

dij是处理不了同时存在异号的边权，建议重新看一下dij不能处理的反例

南岸以南南岸哀 2022-07-28 00:07

妙呀

bw 2022-05-29 20:35

mark

pydmy7 2022-03-01 20:52

for(int i=1,z=0;i<=k;i++)
        add(i*n,(i+1)*n,z);
    //如果读者认真观察代码的话一定会问为什么要有如此操作
    //那么读者仔细思考，若无此操作，如果有一组数据 1 到 N 经过的边小于 k ，会发生什么呢？

其实这一步不是必须的，一种替代的方法是直接从第0层到第k层统计(最小值)答案

Moyou 2022-12-27 19:34

支持

炽热小老弟 2023-08-12 21:20 回复了 Moyou 的评论

做完最短路之后枚举答案是吗？

pydmy7 2022-03-01 20:48

“如果经过的边数小于 K ，花费为 0” —> “如果经过的边数小于等于 K ，花费为 0”

尼斯湖水怪 2022-01-23 17:53

Orz

Gzm1317 2021-10-27 12:50

### 我去!Orz

ewoifuoi 2021-10-16 21:17

tql%%%

xhk 2021-05-11 10:34

tql

铁 2021-03-17 20:22

太巧妙了，思路无敌

    for(int i=1,z=0;i<=k;i++)
        add(i*n,(i+1)*n,z);
    //如果读者认真观察代码的话一定会问为什么要有如此操作
    //那么读者仔细思考，若无此操作，如果有一组数据 1 到 N 经过的边小于 k ，会发生什么呢？

尤其是这段代码，防止了边数<=k的情况的错误(ORZ)

zhaojw_ 2021-09-10 16:33

加上这一段代码就代表着最终答案答案一定在k+1层图下的第n个点也就是dist[(k + 1) * n]
当然也可以不加这一段,在每一层的第n个点找最小的值
不加这一段代码:

 int res = 0x3f3f3f3f;
    for(int i = 0; i <= n; i ++)
        res = min(res, dist[i * n]);
    if(res == 0x3f3f3f3f)puts("-1");
    else cout << res << "\n";