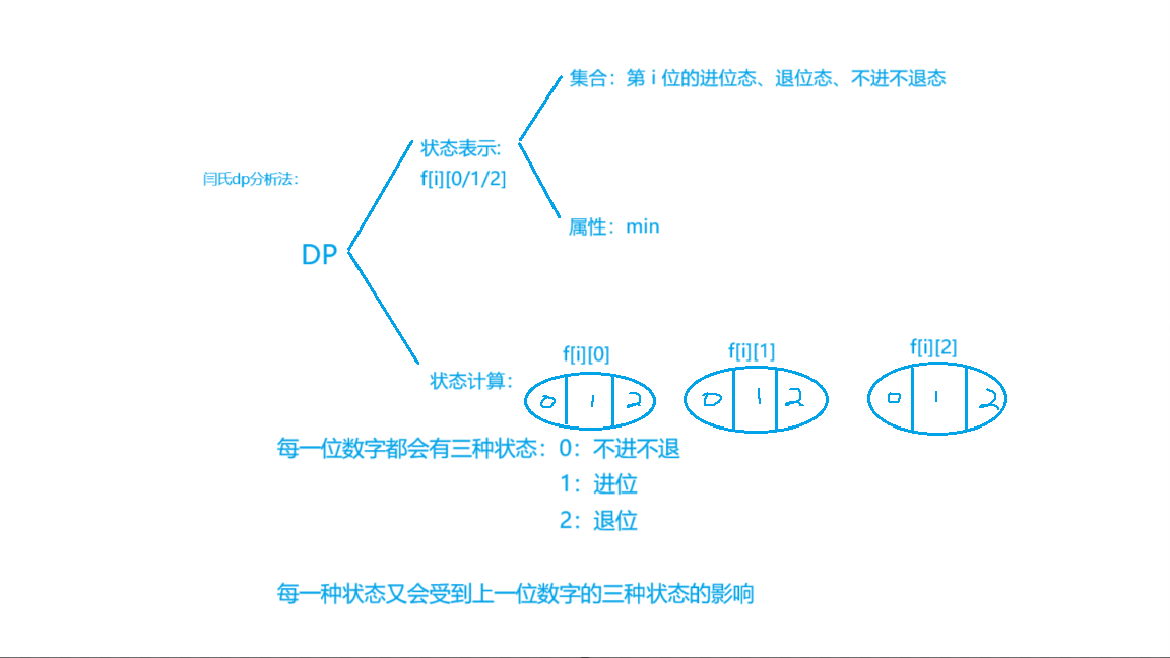
用𝑓[𝑖][0]、𝑓[𝑖][1]和𝑓[𝑖][2]表示当前位不进不退、当前位通过加法发生进位和当前位通过减法发生退位需要操作的最少次数。为了达成该位只受上一位的状态的影响，故此我们需要从右往左遍历（用num_𝑥表示文本串当前位的数字，用 num_𝑦 表示模板串当前位的数字）：

• 显而易见的不进不退时的操作次数 = 𝑎𝑏𝑠(num_x - num_y)
• 而进位时的操作次数应为 10 + (num_y - num_x)
  • 即模板数减去文本数 如 2 -> 7： 2进位成 17 就要 加上10 +（7 - 2），再如8 -> 3： 8进位成 13 就要 加上10 + （8 - 3）且上一位有产生退位或者进位时，需要让 num_x - 1/+ 1
• 退位时应为 10 + num_x - num_y
  • 即文本数减去模板数 如 2 -> 7： 2退位成 “- 7” 就要 减去10 +（2 - 7），再如8 -> 3： 8退位成 “-3” 就要 减去10 + （3 - 8）且上一位有产生退位或者进位时，需要让 num_x - 1/+ 1

• 而最重要的初始化也要很清晰，初始的个位没有上一位的进位退位影响

• 当前位没有发生进位𝑓[𝑖+1][0](这里我从 i + 1 开始，规定 f[0] 是个位)：
  （1）上一位操作完了之后当前位没有发生改变，那么：
  当前位不进位需要操作的次数即为：step1 = 𝑓[𝑖][0]+𝑎𝑏𝑠(num_x - num_y)。
  （2）上一位操作完了之后当前位增大了一位，那么：
  当前位不进位需要操作的次数即为：step2 = 𝑓[𝑖][1]+𝑎𝑏𝑠(num_x - num_y + 1)。
  （3）上一位操作完了之后当前位减小了一位，那么：
  当前位不进位需要操作的次数即为：step3 = 𝑓[𝑖+1][2]+𝑎𝑏𝑠(num_x - num_y - 1)。
  综上：f[i + 1][0] = min(step1, step2, step3)。

• 当前位的数通过加法进位𝑓[𝑖+1][1]：
  （1）上一位操作完了之后当前位没有发生改变，那么：
  当前位通过加法进位需要操作的次数即为：step1 = f[i][0] + 10 + num_y - num_x。
  （2）上一位操作完了之后当前位增大了一位，那么：
  当前位通过加法进位需要操作的次数即为：step2 = f[i][1] + 10 + num_y - (num_x + 1)。
  （3）上一位操作完了之后当前位减小了一位，那么：
  当前位通过加法进位需要操作的次数即为：step3 = f[i][2] + 10 + num_y - (num_x - 1)。
  综上：f[i + 1][1] = min(step1, step2, step3)。
• 当前位的数通过减法退位𝑓[𝑖+1][2]：
  （1）上一位操作完了之后当前位没有发生改变，那么：
  当前位通过减法退位需要操作的次数即为：step1 = f[i][0] + 10 + num_x - num_y。
  （2）上一位操作完了之后当前位增大了一位，那么：
  当前位通过减法退位需要操作的次数即为：step2 = f[i][1] + 10 + (num_x + 1) - num_y。
  （3）上一位操作完了之后当前位减小了一位，那么：
  当前位通过减法退位需要操作的次数即为：step3 = f[i][2] + 10 + (num_x - 1) - num_y。
  综上：f[i + 1][2] = min(step1, step2, step3)。

最终答案即为𝑚𝑖𝑛(f[n - 1][0], f[n - 1][1], f[n - 1][2])。

n = int(input())
x = input()
y = input()
f = [[0, 0, 0] for _ in range(n + 1)]  # 不能直接[[0, 0 , 0]] * (n + 1)
f[0] = [abs(int(x[n - 1]) - int(y[n - 1])), 10 + int(y[n - 1]) - int(x[n - 1]), 10 + int(x[n - 1]) - int(y[n - 1])]

for i in range(n - 1):
    num_x = int(x[n - 2 - i])
    num_y = int(y[n - 2 - i]) 
    # 第i位不进不退的状态(因为我把循环规定了从0开始，所以加1)
    step1 = f[i][0] + abs(num_x - num_y)  # 上一位不进不退   
    step2 = f[i][1] + abs(num_x - num_y + 1)  # 上一位进位
    step3 = f[i][2] + abs(num_x - num_y - 1)  # 上一位退位
    f[i + 1][0] = min(step1, step2, step3)

    # 第i位进位的状态
    step1 = f[i][0] + 10 + num_y - num_x  # 上一位不进不退   
    step2 = f[i][1] + 10 + num_y - (num_x + 1)  # 上一位进位
    step3 = f[i][2] + 10 + num_y - (num_x - 1)  # 上一位退位
    f[i + 1][1] = min(step1, step2, step3)

    # 第i位退位的状态
    step1 = f[i][0] + 10 + num_x - num_y  # 上一位不进不退   
    step2 = f[i][1] + 10 + (num_x + 1) - num_y   # 上一位进位
    step3 = f[i][2] + 10 + (num_x - 1) - num_y   # 上一位退位
    f[i + 1][2] = min(step1, step2, step3)

ans = min(f[n - 1][0], f[n - 1][1], f[n - 1][2])
print(ans)