思路

转换成图问题，将每一个瓶子看作一个点，每个瓶子向它应该在的位置上的瓶子连接一条边，会形成一堆环

特点:

n个点，n条边，每个点的出度、入度均为1(每个点指向的该正确摆放该点的位置唯一、每个点的位置也只能被另一个点指向来正确摆放另一个点)。鉴于此特点，不会出现分岔，则必然是一堆环(每个环称作一个置换)

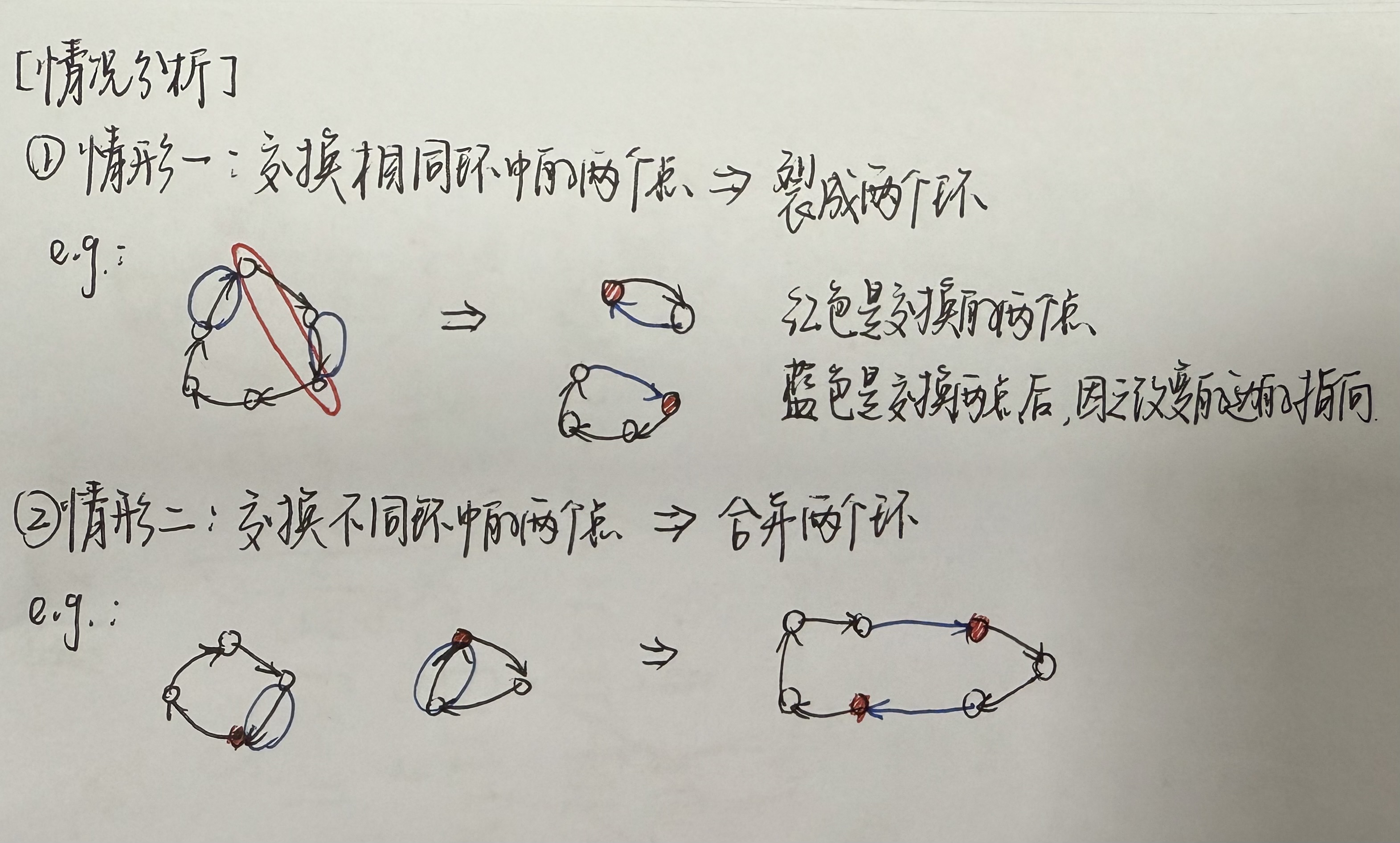
交换情况辨析:

始末态分析:

显然，要从最开始的k个环变成最后的n个自环，每次操作至多增加1个环，故至少进行n-k次操作，即只要知道初始状态的环数即可立即算出题设答案

注意

1.与小朋友排队这题不同，小朋友那道题每次只能交换相邻的元素，交换次数即逆序对个数(至多n^2级别，完全逆序时每对坐标都构成逆序对)；本题可以交换任意位置上的两个元素，类似选择排序，每次选好一个数摆在正确的位置，故此题的交换次数至多为n-1(摆好n-1个数时，剩下一个已然放好)

2.虽然代码中有两重循环，但是判重数组st保证了每个点至多遍历一次，总时间复杂度$O(n)$

代码

#include<bits/stdc++.h>
using namespace std;

const int n = 10010;
int b[n];
bool st[n];
int N;

int main()
{
    cin >> N;
    for(int i = 1;i <= N;i ++) cin >> b[i];

    int cnt = 0;    // 记录初始状态下环的个数
    for(int i = 1;i <= N;i ++) // 遍历每一个点
        if(!st[i])  // 该点没有被找过 说明这个点在一个新的环里
        {
            cnt++;  // 环的个数 + 1
            for(int j = i;!st[j];j = b[j])  // 将这个环包含的所有点都找到
                st[j] = true;   // 标记这些点为已找到
        }
    cout << N - cnt;    // 最终状态下的自环数 - 初始状态下的环数
    return 0;
}