qwq

我的博客

题目

给你一棵TREE,以及这棵树上边的距离.问有多少对点它们两者间的距离小于等于K

输入输出格式
输入格式：
N（n<=40000） 接下来n-1行边描述管道，按照题目中写的输入 接下来是k

输出格式：
一行，有多少对点之间的距离小于等于k

输入输出样例
输入样例#1：

7
1 6 13 
6 3 9 
3 5 7 
4 1 3 
2 4 20 
4 7 2 
10

输出样例#1：

5

题解

• lrd大佬讲课时因为听不懂，翻书水时间的时候看到了点分治，就学了一下qwq
• 首先对于这道题一个很暴力的想法：枚举每个点对看看之间的距离是否$\leq k$，复杂度应该是$O(n^2logn)?$
• 暴力的思路显然过不了我这种暴力选手该怎么办啊qwq
• 我们考虑树上两点之间的路径有什么情况
  1. 经过根节点
  2. 不经过根节点
• 对于第一种的情况我们算两点间路径长度时可以将$dis(u,v)$转化为$dis(u,root)+dis(root,v)$
• 而对于第二种情况我们可以找到$u,v$路径所在的子树，将根节点变为子树的根节点，然后就变为了第一种情况
• 所以我们可以不断的递归根节点将所有情况转化为第一种情况
• 设$belong[u]$表示$u$属于哪一棵子树
• 那么$belong[u]=\not belong[v] \quad d[u]+d[v]\leq k$满足条件的第一类路径条数即为满足条件的点对数
• 下面我们来讨论如何计算满足条件的点对数：
  1. 将树中的节点到根节点的权值放入数组$len$中，并排序
  2. 用两个指针$l,r$扫描数组，每找到一个合法的答案就加上$r-l$，就让$l++$，否则让$r–
• 对于上面的计算我们发现有一些问题（如下图有点丑）：
  
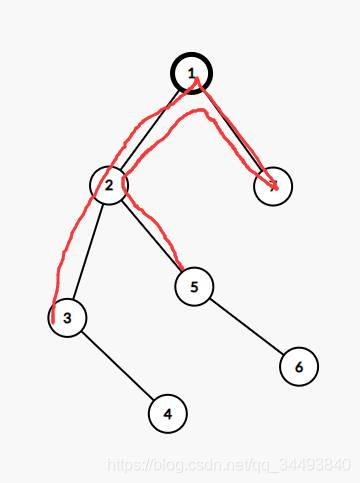
• 在指针扫描的过程中我们会出现不合法（关于合法的判断请看上面的条件）的情况
• 这该怎么办呢嘤嘤嘤
• 我们可以发现不合法的路径在当前根的一颗子树上，即没有跨越两棵子树（如果跨越了它就合法了）
• 所以们可以在遍历的时候减去不合法的情况（容斥）
• 具体的方法
  1. $all += cal(x,0)$
  2. $all -= cal(v,dis(u,v))$
• 讲解：
• 一个蒟蒻的口胡可以求当前根节点的儿子节点的答案，统计儿子节点的答案时将各个点的距离加上儿子到根节点的距离，即把符合在一个子树条件的情况统计出来，即不合法的答案，最后用根节点算出来的总答案减去不合法的答案就行了。可以结合上面那个不合法的图理解一下（如果不合法的话两点会多了两倍到根节点的距离，在遍历儿子节点时将每个点到根节点的距离都加上儿子节点距离就和不合法的情况相同了）
• 点分治的关键之处是在递归根节点的过程，我们每次将根节点选为重心会将复杂度降低，因为最差情况也只会递归$logn$层，其余情况最差可能达到$n$层
• 点分治的复杂度为$Onlog^2n$，比较优秀qwq

#include <map>
#include <set>
#include <list>
#include <cmath>
#include <deque>
#include <queue>
#include <stack>
#include <cctype>
#include <string>
#include <cstdio>
#include <vector>
#include <complex>
#include <cstring>
#include <iomanip>    
#include <iostream>
#include <algorithm>
#include <functional>
using namespace std; 
typedef long long LL; 
const int maxn = 40000 + 100; 

template <class T> 
inline void read(T &s) {
    s = 0; 
    T w = 1, ch = getchar(); 
    while (!isdigit(ch)) { if (ch == '-') w = -1; ch = getchar(); }
    while (isdigit(ch)) { s = (s << 1) + (s << 3) + (ch ^ 48); ch = getchar(); }
    s *= w; 
}

int n, m, k, tot, all_node, ans, root;
// root 为重心
// ans 为答案
// all_node 表示所有点的数目 
int lin[maxn], max_part[maxn], size[maxn], len[maxn], d[maxn]; 
// d[i] 表示i到根节点的距离
// len[i] 表示路径长度
// len[0] 中记录节点个数
// size[i] 表示以i为根的子树大小
// max_part[i] 表示i的最大的子树大小
bool vis[maxn]; 
// vis用于求重心时避免重复访问 
struct node {
    int next, to, dis; 
} edge[maxn << 1]; 
// edge 用于存边

inline void add(int from, int to, int dis) {
    edge[++tot].to = to; 
    edge[tot].dis = dis; 
    edge[tot].next = lin[from]; 
    lin[from] = tot; 
}

void get_root(int u, int fa) { // 找到树的重心
    max_part[u] = 0, size[u] = 1; 
    for (int i = lin[u]; i; i = edge[i].next) {
        int v = edge[i].to; 
        if (v == fa || vis[v]) continue;  
        get_root(v, u); 
        size[u] += size[v]; 
        max_part[u] = max(max_part[u], size[v]); 
    }
    max_part[u] = max(max_part[u], all_node - size[u]); 
    if (max_part[u] < max_part[root]) root = u; 
}

void get_dis(int u, int fa) { // 求出每个点到根节点的距离
    len[++len[0]] = d[u]; 
    for (int i = lin[u]; i; i = edge[i].next) {
        int v = edge[i].to; 
        if (v == fa || vis[v]) continue; 
        d[v] = d[u] + edge[i].dis; 
        get_dis(v, u); 
    }
}

int cal(int u, int now) { // 计算以u为根的所有情况的答案
    d[u] = now, len[0] = 0; 
    get_dis(u, 0); 
    sort(len + 1, len + len[0] + 1); 
    int all = 0; 
    for (int l = 1, r = len[0]; l < r; ) {
        if (len[l] + len[r] <= k) {
            all += r - l; 
            ++l; 
        }
        else r--; 
    }
    return all; 
}

void solve(int u) { // 求解以u为重心的情况
    vis[u] = true; 
    ans += cal(u, 0); 
    for (int i = lin[u]; i; i = edge[i].next) {
        int v = edge[i].to; 
        if (vis[v]) continue; 
        ans -= cal(v, edge[i].dis); // 减去不合法的
        all_node = size[v]; 
        root = 0; 
        get_root(v, u); 
        solve(root); 
    }
}

int main() {
    while (1) {
        read(n), read(k); 
        if (!n && !k) break; 

        tot = 0; ans = 0; 
        memset(lin, 0, sizeof(lin)); 
        memset(max_part, 0, sizeof(max_part)); 
        memset(size, 0, sizeof(size)); 
        memset(vis, false, sizeof(vis)); 

        for (int i = 1; i < n; ++i) {
            int u, v, w; 
            read(u), read(v), read(w); 
            add(u+1, v+1, w); 
            add(v+1, u+1, w); 
        }
        // read(k); 
        all_node = n, max_part[0] = n, root = 0; 
        get_root(1, 0); 
        solve(root); 
        printf("%d\n", ans); 
    }
    return 0; 
}