AcWing 1206. 剪格子(含AC注释代码)    原题链接    困难

作者： 作者的头像   KaMtuo ,  2021-02-16 14:52:55 ,  所有人可见 ,  阅读 3750

28


8

题目描述

如下图所示，3×3 的格子中填写了一些整数。

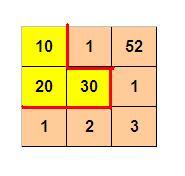
19_b005932413-p1.jfif

我们沿着图中的红色线剪开，得到两个部分，每个部分的数字和都是 60。

本题的要求就是请你编程判定：对给定的$ m×n$ 的格子中的整数，是否可以分割为两个连通的部分，使得这两个区域的数字和相等。

如果存在多种解答，请输出包含左上角格子的那个区域包含的格子的最小数目。

如果无法分割，则输出 0。

19_ebc01ba013-p2.jfif

输入格式

第一行包含两个整数 $m,n$ ,表示表格的宽度和高度。

接下来是 $n$ 行，每行$ m$ 个正整数，用空格分开。

输出格式

在所有解中，包含左上角的分割区可能包含的最小的格子数目。

如果无法分割，则输出$ 0$。

数据范围

$1≤n,m<10$,
格子内的数均在$1$到$10000$之间。

输入样例1：

3 3
10  1 52
20 30  1
 1  2  3

输出样例1：

3

输入样例2：

4 3
1  1  1   1
1 30 80   2
1  1  1 100

输出样例2：

10

算法1

蓝桥杯官网AC：

蓝桥杯官网仅包含了以左上角为起点，可不重复一笔画完成的裁剪数据，比如题目描述中的图一。
DFS搜索即可，本题解着重讲解Acwing AC代码，对此不做更多描述。

蓝桥杯AC代码

#include<bits/stdc++.h>
using namespace std;
const int N=20;
int dx[]={0,0,1,-1},dy[]={1,-1,0,0};
int sum;
int ans=INT_MAX;
int n,m;
int val[N][N];
bool st[N][N];
void dfs(int x,int y,int cnt,int v){
   if(v==sum/2){
       ans=min(ans,cnt);
       return;
    }
    if(v>sum/2)return;
    for(int i=0;i<4;i++){
        int a=x+dx[i],b=y+dy[i];
        if(a<1||b<1||a>m||b>n)continue ;
        if(st[a][b]==true)continue;
        st[a][b]=true;
        dfs(a,b,cnt+1,v+val[a][b]);
        st[a][b]=false;
    }
}
int main(){
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        for(int j=1;j<=n;j++){
            scanf("%d",&val[i][j]);
            sum+=val[i][j];
        }
    }
    if(sum%2==0){
        st[1][1]=true;
        dfs(1,1,1,val[1][1]);
    }
    printf("%d",ans==INT_MAX?0:ans);
    return 0;
}

算法2

Acwing AC ：

首先对题意进行理解：
两个连通的部分，即分别在所分割的两部分中，任何一个点都能合法到达该部分的所有位置。
如下图所示，红色部分点与点之间都至少存在一条位于红色内部的路径，黄色部分同理。表明其为两个连通的部分。
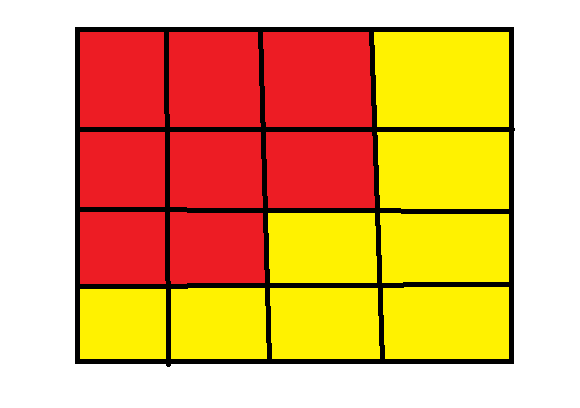
QQ图片20210216113427.png
如下图所示，展示的是两种不合法情况。
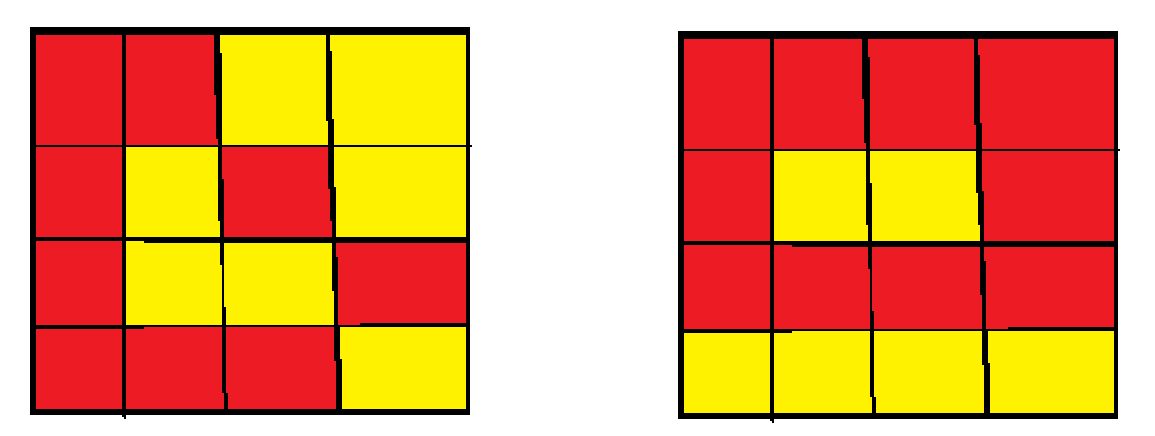
QQ图片20210216114432.png

使得这两个区域的数字和相等，这是本题搜索的依据，两个区域数字和相等，且只能分割为两个连通的部分，易得出如果存在这样的两个部分，那么该图中元素总和必为偶数，且每个部分中元素和是元素总和的一半，可得元素总和为奇数时，一定无法分割成满足条件的情况。
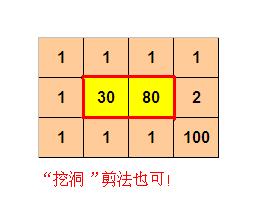
如下图所示，元素总和为$60$，每个部分中元素和均为$30==60/2$
19_b005932413-p1.jfif

包含左上角格子的那个区域包含的格子的最小数目，意味着也许包含多种分割方式满足条件，可能需要对所有情况进行搜索找出最小格子数，故本题解选择DFS进行搜索。若要满足包含左上角格子的条件，只需以左上角为起点开始搜索即可，并且过程中均是以合法路径进行搜索，故搜索部分一定是连通的，只需要判断剩余部分是否连通即可。

判断剩余部分是否连通

采用宽度搜索，连通也可体现为以当前部分中任一点为起点，可到达当前部分所有点，故在元素和满足条件时，找到任意一个未使用的格子，以此格子为起点，求出它能到达的所有未使用格子数，再将其与搜索格子数和总格子数进行比较，判断是否满足条件。

分支思路

按照通常的深度搜索思路，每次都是由一个点开始进行搜索，搜索出的路径没有支线的存在，而本题中，可能存在一条甚至多条支线，故传统的深度搜索无法满足要求。在本题中，我们将每个搜索到的格子存入一个集合中，在每一次搜索时遍历该集合中的所有格子，并以各个格子为当前起点进行搜索，这就达到了分支的目的。

而分支导致的问题也显而易见————时间复杂度太大了，我用一开始未进行优化的代码跑了一下$5×5$的数据，跑了半小时没跑出来，所以剪枝优化就成了必不可少的步骤。

很多剪枝容易想到和实现：比如因为题目中给出的数据范围，权值必为正数，所以当元素和大于目标值时，便可提前结束；因为是求最小格子数，所以搜索格子数大于等于当前答案时，可提前结束；因为相同方案的格子数和元素和相同，所以用哈希表查重，当方案已出现时，提前结束。不过加入了这三种优化依旧TLE，可以想象一下我当时的绝望hhh。

优化

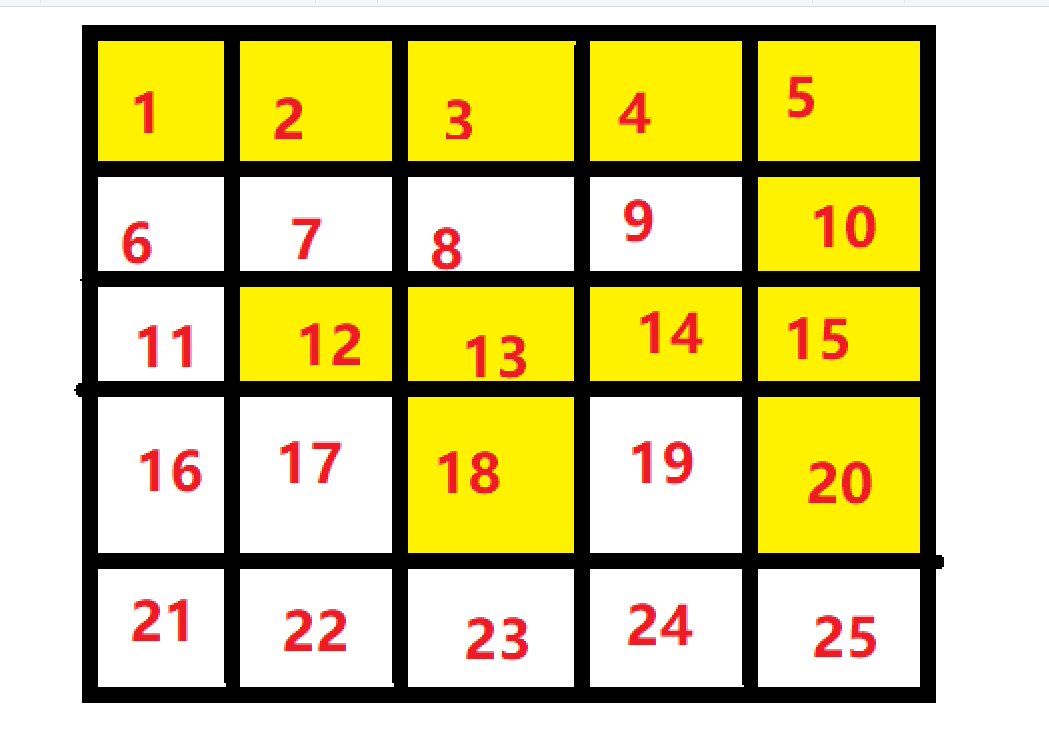
如下图所示
黄色部分为已搜索区域，数字表示编号（不是权重），假设此时搜索并未结束。
当前搜索集合为{1,2,3,4,5,10,12,13,14,15,18,20}，下次搜索加入的格子编号可能是$6,7,8,9,11,17,19,23,25$，而因为集合中所有格子都会进行一轮搜索，其中有些格子会被多次搜索，比如$19$这个格子，会被$14,18,20$分别搜索一次，但其产生的结果却是一样的，进行了重复计算，所以我在深度搜索中加入了一个布尔数组，标记当前集合每个已被使用的格子，比如$19$在$14$搜索时被使用过，当即将其标记，则在$18,20$搜索时不会被搜索到，保证每个格子只使用一次。至此，已经可以AC。
QQ图片20210216132821.png

不过我实在是太闲了，于是又去看了下y总的代码，发现有一部分代码是我完全看不懂的，这表明y总想到了我难以想到的地方，这题目还有优化的空间！！！于是我又开始研究y总的代码。

y总的优化

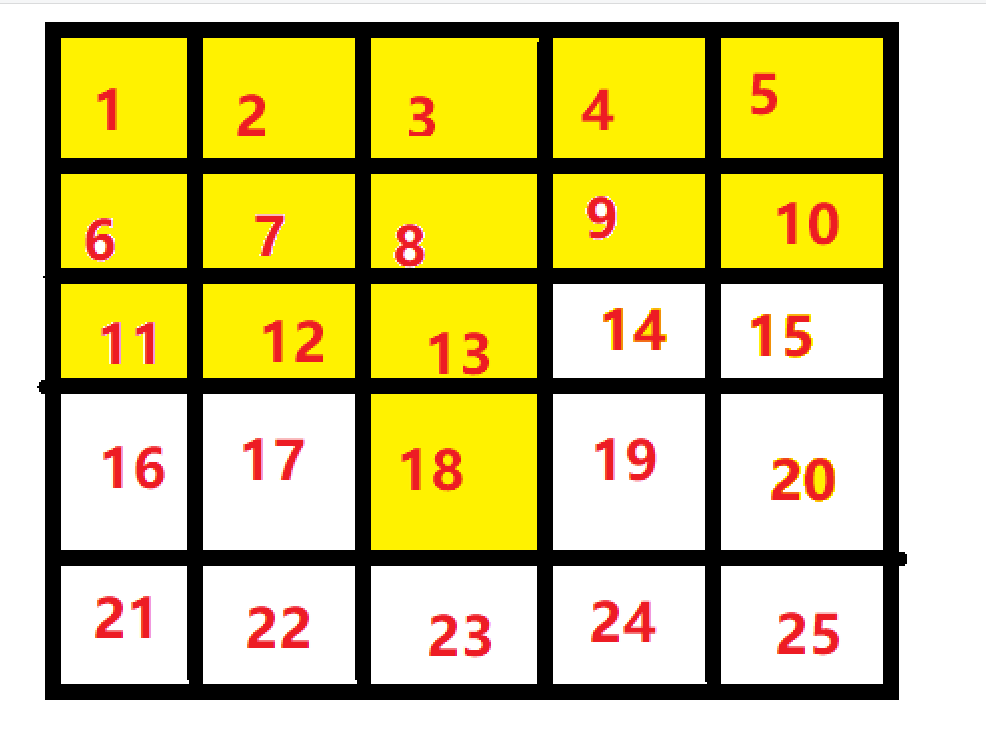
如下图所示
当前搜素集合为{1,2,3,4,5,6,7,8,9,10,11,12,13,18}，如果按集合顺序进行搜索，从图中可看出$1$到$8$格子已经没有搜索的余地了，但依旧会占据一部分运算时间。而因为本题是从左上角开始搜索，每次集合中的上升趋势大概率大于集合中的下降趋势，所以将集合编号（二维坐标可能更明显）从大到小进行排序，可使每次搜索能更快接近答案。
QQ图片20210216140315.png

y总代码在其他题解可以找到，这里讲一下大家可能的疑问
y总在这一段优化代码中进行了判重，而我却没有，这主要得益于我在优化时加入的布尔数组，保证了bkt(对应于y总的points)中不含重复元素，所以不需要进行判重。

    //y总
    sort(points.begin(), points.end());
    reverse(points.begin(), points.end());
    for(int i = 0; i < points.size(); ++ i)
        if(!i || points[i] != points[i - 1])//判重
            {
                int a = points[i].first, b = points[i].second;
                cands[k] = points[i];
                st[a][b] = true;
                dfs(s + w[a][b], k + 1);
                st[a][b] = false;
            }


    sort(bkt.begin(),bkt.end(),cmp);//从大到小排序
    for(int i=0;i<bkt.size();i++){//按从大到小的顺序进行搜索
        lo.push_back(bkt[i]);//插入
        int x=(bkt[i]-1)/n+1,y=(bkt[i]-1)%n+1;//获得二维坐标
        st[x][y] = true;//标记使用
        dfs(cnt+1,v+val[x][y], lo);
        lo.pop_back();//恢复现场
        st[x][y] = false;//恢复现场
    }
}

最终代码

#include<bits/stdc++.h>
using namespace std;
const int N=20,P=131;
int dx[]={0,0,1,-1},dy[]={1,-1,0,0};//偏移量
int sum;//元素总和
int ans=INT_MAX;//答案
int n,m;
int val[N][N];//每个格子的权重
bool st[N][N];//在路径搜索中每个格子是否使用
bool ct[N][N];//判断剩余部分是否连通时，格子是否使用
unordered_set<unsigned long long> se;//哈希表查重
vector<int>loc;//一维存储格子编号 如：二维坐标为(1,2)的点一维编号为2
vector<int>los;//一维存储格子编号
int cot;
int turn(int x,int y){ //计算一维编号
    return (x-1)*n+y;
}
bool bfs(int cnt){//宽度搜索(从一个点开始搜索其连通的所有未使用点) 用于判断剩余部分是否连通。
                //cnt : 表示搜索部分包含的格子数
    while(!loc.empty()){
        int si=loc.size()-1;
        int id=loc[si];//在末尾获得一维编号
        int x=(id-1)/n+1,y=(id-1)%n+1;//计算二维坐标
        loc.pop_back();//将末尾元素移除
        for(int i=0;i<4;i++){
            int a=x+dx[i],b=y+dy[i];
            if(a<1||b<1||a>m||b>n)continue ;//越界
            if(ct[a][b]==true)continue;//已使用
            cot++;//计算当前格子数
            loc.insert(loc.begin(),turn(a,b));//将该点编号插入头部，用于下次搜索
            ct[a][b]=true;//标记使用
        }
    }
    if(cot+cnt==m*n)return true;//如果剩余部分连通格子数量与搜索部分格子数量和为总格子数，
                                //则表明其被分割成两个连通的部分。
    return false;
}
bool check(vector <int>u){//哈希表查重
    sort(u.begin(),u.end());
    unsigned long long x = 0;
    for (int i = 0; i < u.size(); i ++ ){
        x=x*P+(u[i]-1)/n+1;
        x=x*P+(u[i]-1)%n+1;
    }
    if (se.count(x)) {
        return true;//如果该方案已存在，返回
    }
    se.insert(x);//插入新方案
    return false;
}
bool cmp(int a,int b){//从大到小排序
    return b<a;
}
void dfs(int cnt,int v,vector<int>lo){//cnt 格子数 。v 当前元素和 。lo 当前包含格子编号集合
     if(v==sum/2){//如果元素和满足要求
       cot=0;//初始化剩余部分格子数
       memcpy(ct,st,sizeof st);
       for(int i=1;i<=m;i++){
         if(loc.size())break;//找到一个未使用格子就跳出循环
                            //(连通也可看作以任意一个处于该部分的格子为起点，可到达该部分所有格子)
           for(int j=1;j<=n;j++){
              if(ct[i][j]==false){//找到未使用格子
                  loc.push_back(turn(i,j));//插入
                  cot++;
                  ct[i][j]=true;//标记使用
                  break;
              }
           }
        }
       if(bfs(cnt)==true){//如果该格子能到达的格子数满足要求，更新答案
         ans=min(ans,cnt);
        }
        return;
    }
    if(v>=sum/2)return;//如果当前元素和已经大于元素总和一半，直接返回
    if(cnt==m*n)return;//如果搜索格子包括所有格子
    if(check(lo))return;//如果当前方案已经出现过
    bool fr[200];//在当前搜索中避免重复搜索
    memset(fr,false,sizeof fr);//初始化
    int len=lo.size();
    vector<int>bkt;//存储当前搜索到格子的一维坐标
    bkt.clear();
    for(int k=0;k<len;k++){
        int p=lo[k];//以所有当前已搜索格子为起点依次搜索
        int x=(p-1)/n+1,y=(p-1)%n+1;
        fr[turn(x,y)]=true;//标记使用
            for(int i=0;i<4;i++){
                int a=x+dx[i],b=y+dy[i];
                if(a<1||b<1||a>m||b>n)continue;//越界
                if(st[a][b]==true)continue;//如果已使用
                if(fr[turn(a,b)]==true)continue;//如果已使用
                if(cnt+1>=ans)continue;//此方案答案不能小于当前答案
                fr[turn(a,b)]=true;//标记使用
                bkt.push_back(turn(a,b));//插入搜索到的格子
            }
    }

    //y总的优化，如果不懂可将题解提供的dfs函数直接复制替换本代码中的dfs函数,也能AC,优化方法不唯一,没有最好的。
    //主要理解这种多笔画的搜索方式。
    sort(bkt.begin(),bkt.end(),cmp);//从大到小排序
    for(int i=0;i<bkt.size();i++){//按从大到小的顺序进行搜索
        lo.push_back(bkt[i]);//插入
        int x=(bkt[i]-1)/n+1,y=(bkt[i]-1)%n+1;//获得二维坐标
        st[x][y] = true;//标记使用
        dfs(cnt+1,v+val[x][y], lo);
        lo.pop_back();//恢复现场
        st[x][y] = false;//恢复现场
    }
}
int main(){
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        for(int j=1;j<=n;j++){
            scanf("%d",&val[i][j]);
            sum+=val[i][j];
        }
    }
    if(sum%2==0){//偶数才可能有答案
        st[1][1]=true;
        los.push_back(turn(1,1));
        dfs(1,val[1][1],los);//已左上角格子为起点搜素
    }
    printf("%d",ans==INT_MAX?0:ans);
    return 0;
}

加一个手写哈希表的代码

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cmath>
#include<climits>
#include<cstring>
#include<vector>
using namespace std;
const int N=20;
const int M=1001001;
int dx[]={0,0,1,-1},dy[]={1,-1,0,0};//偏移量
int sum;//元素总和
int ans=INT_MAX;//答案
int h[M],idx,ne[M];
unsigned long long d[M];
int n,m;
int val[N][N];//每个格子的权重
bool st[N][N];//在路径搜索中每个格子是否使用
bool ct[N][N];//判断剩余部分是否连通时，格子是否使用
vector<int>loc;//一维存储格子编号 如：二维坐标为(1,2)的点一维编号为2
vector<int>los;//一维存储格子编号
int cot;
int turn(int x,int y){ //计算一维编号
    return (x-1)*n+y;
}
//往哈希表里添加元素（拉链法）
void add(unsigned long long  u){
    ne[idx]=h[(int)(u%M)];
    d[idx]=u;
    h[(int)(u%M)]=idx++;
}
//查重
int find(unsigned long long u){
    for(int i=h[(int)(u%M)];~i;i=ne[i]){
        if(d[i]==u)return 1;
    }
    return 0;
}
bool bfs(int cnt){//宽度搜索(从一个点开始搜索其连通的所有未使用点) 用于判断剩余部分是否连通。
                //cnt : 表示搜索部分包含的格子数
    while(!loc.empty()){
        int si=loc.size()-1;
        int id=loc[si];//在末尾获得一维编号
        int x=(id-1)/n+1,y=(id-1)%n+1;//计算二维坐标
        loc.pop_back();//将末尾元素移除
        for(int i=0;i<4;i++){
            int a=x+dx[i],b=y+dy[i];
            if(a<1||b<1||a>m||b>n)continue ;//越界
            if(ct[a][b]==true)continue;//已使用
            cot++;//计算当前格子数
            loc.insert(loc.begin(),turn(a,b));//将该点编号插入头部，用于下次搜索
            ct[a][b]=true;//标记使用
        }
    }
    if(cot+cnt==m*n)return true;//如果剩余部分连通格子数量与搜索部分格子数量和为总格子数，
                                //则表明其被分割成两个连通的部分。
    return false;
}
bool check(vector <int>u){//哈希表查重
    sort(u.begin(),u.end());
    unsigned long long x = 0;
    for (int i = 0; i < u.size(); i ++ ){
        x=x*10+u[i];
    }
    if (find(x)) {
        return true;//如果该方案已存在，返回
    }
    add(x);//插入新方案
    return false;
}
bool cmp(int a,int b){//从大到小排序
    return b<a;
}
void dfs(int cnt,int v,vector<int>lo){//cnt 格子数 。v 当前元素和 。lo 当前包含格子编号集合
     if(v==sum/2){//如果元素和满足要求
       cot=0;//初始化剩余部分格子数
       memcpy(ct,st,sizeof st);
       for(int i=1;i<=m;i++){
         if(loc.size())break;//找到一个未使用格子就跳出循环
                            //(连通也可看作以任意一个处于该部分的格子为起点，可到达该部分所有格子)
           for(int j=1;j<=n;j++){
              if(ct[i][j]==false){//找到未使用格子
                  loc.push_back(turn(i,j));//插入
                  cot++;
                  ct[i][j]=true;//标记使用
                  break;
              }
           }
        }
       if(bfs(cnt)==true){//如果该格子能到达的格子数满足要求，更新答案
         ans=min(ans,cnt);
        }
        return;
    }
    if(v>=sum/2)return;//如果当前元素和已经大于元素总和一半，直接返回
    if(cnt==m*n)return;//如果搜索格子包括所有格子
    if(check(lo))return;//如果当前方案已经出现过
    bool fr[200];//在当前搜索中避免重复搜索
    memset(fr,false,sizeof fr);//初始化
    int len=lo.size();
    vector<int>bkt;//存储当前搜索到格子的一维坐标
    bkt.clear();
    for(int k=0;k<len;k++){
        int p=lo[k];//以所有当前已搜索格子为起点依次搜索
        int x=(p-1)/n+1,y=(p-1)%n+1;
        fr[turn(x,y)]=true;//标记使用
            for(int i=0;i<4;i++){
                int a=x+dx[i],b=y+dy[i];
                if(a<1||b<1||a>m||b>n)continue;//越界
                if(st[a][b]==true)continue;//如果已使用
                if(fr[turn(a,b)]==true)continue;//如果已使用
                if(cnt+1>=ans)continue;//此方案答案不能小于当前答案
                fr[turn(a,b)]=true;//标记使用
                bkt.push_back(turn(a,b));//插入搜索到的格子
            }
    }

    //y总的优化，如果不懂可将题解提供的dfs函数直接复制替换本代码中的dfs函数,也能AC,优化方法不唯一,没有最好的。
    //主要理解这种多笔画的搜索方式。
    sort(bkt.begin(),bkt.end(),cmp);//从大到小排序
    for(int i=0;i<bkt.size();i++){//按从大到小的顺序进行搜索
        lo.push_back(bkt[i]);//插入
        int x=(bkt[i]-1)/n+1,y=(bkt[i]-1)%n+1;//获得二维坐标
        st[x][y] = true;//标记使用
        dfs(cnt+1,v+val[x][y], lo);
        lo.pop_back();//恢复现场
        st[x][y] = false;//恢复现场
    }
}
int main(){
    cin>>n>>m;
    for(int i=0;i<M;i++)h[i]=-1;
    for(int i=1;i<=m;i++){
        for(int j=1;j<=n;j++){
            scanf("%d",&val[i][j]);
            sum+=val[i][j];
        }
    }
    if(sum%2==0){//偶数才可能有答案
        st[1][1]=true;
        los.push_back(turn(1,1));
        dfs(1,val[1][1],los);//已左上角格子为起点搜素
    }
    printf("%d",ans==INT_MAX?0:ans);
    return 0;
}

未加入y总优化的dfs函数

void dfs(int cnt,int v,vector<int>lo){
     if(v==sum/2){
       cot=0;
       memcpy(ct,st,sizeof st);
       for(int i=1;i<=m;i++){
         if(loc.size())break;
           for(int j=1;j<=n;j++){
              if(ct[i][j]==false){
                  loc.push_back(turn(i,j));
                  cot++;
                  ct[i][j]=true;
                  break;
              }
           }

       }
       if(bfs(cnt)==true){
         ans=min(ans,cnt);
        }
        return;
    }
    if(v>=sum/2)return;
    if(cnt==m*n)return;
    if(check(lo))return;
    bool fr[200];
    memset(fr,false,sizeof fr);
    int len=lo.size();
    for(int k=0;k<len;k++){
        int p=lo[k];
        int x=(p-1)/n+1,y=(p-1)%n+1;
        fr[turn(x,y)]=true;
            for(int i=0;i<4;i++){
                int a=x+dx[i],b=y+dy[i];
                if(a<1||b<1||a>m||b>n)continue;
                if(st[a][b]==true)continue;
                if(fr[turn(a,b)]==true)continue;
                if(cnt+1>=ans)continue;
                st[a][b]=true;
                fr[turn(a,b)]=true;
                lo.push_back(turn(a,b));
                dfs(cnt+1,v+val[a][b],lo);
                lo.pop_back();
                st[a][b]=false;
            }
    }
}

第一次写题解，如果发现错误，请在评论中指出。（转载请注明出处与链接）

25 评论

用户头像
小Y不敲代码   2023-03-23 11:09      5    踩      回复

大佬太强了，不过这道题不适合我

用户头像
RwChen   2022-04-05 15:57         踩      回复

深搜必须有起点，这题数据好恶心，起点可能不是1,1

用户头像
此账号已注消   2022-04-08 17:02         踩      回复

分成两个部分，所以说一个连通块一定包含(1 , 1),从(1 , 1)爆搜为什么不可？

用户头像
此账号已注消   2022-04-08 17:02         踩      回复

起点必定为(1,1）不包含我们把当前连通块看成另一个连通块去爆搜啊

用户头像
RwChen   2022-04-08 18:07    回复了 此账号已注消 的评论         踩      回复

10 10 10
10 20 10
10 20 20
你从1，1开始怎么搜

用户头像
此账号已注消   2022-04-08 18:39    回复了 RwChen 的评论         踩      回复

为什么不能从(1,1)搜啊？这不是一笔画问题，是连通块问题

用户头像
此账号已注消   2022-04-08 18:41    回复了 RwChen 的评论         踩      回复

最后答案是选择包含左端点(1,1)的个数

用户头像
此账号已注消   2022-04-08 18:42    回复了 RwChen 的评论         踩      回复

您是不是理解错题了，我猜你可能以为答案是3，应该是4((1,1) , (1,2),(2,2),(3,2))的

用户头像
此账号已注消   2022-04-08 18:42    回复了 RwChen 的评论         踩      回复

如果存在多种解答，请输出包含左上角格子的那个区域包含的格子的最小数目。

用户头像
RwChen   2022-04-08 22:38    回复了 此账号已注消 的评论         踩      回复

你从（1,1）这个点搜不过去的，dfs又不能同时往两边搜，因为dfs是搜一笔画，但（1,1）开始搜不出一笔画的答案，那个角不是dfs能搜出来的

用户头像
RwChen   2022-04-08 22:39    回复了 此账号已注消 的评论         踩      回复

这个答案很明显是那几个十，但你能用你写的dfs把这个搜出来吗

用户头像
KaMtuo   2022-04-09 00:01    回复了 RwChen 的评论         踩      回复

不能一笔画出来。你们俩互相的理解应该是不同的2333，你看我代码里的dfs，就是把（1,1）作为起点丢进去，就看怎么理解了，常规dfs肯定不能这样搞出来hh，你俩说的都没错，没必要争了hh，感谢讨论。

用户头像
努力挣钱   2021-10-21 16:30         踩      回复

$if(cnt+1>=ans)continue$;//此方案答案不能小于当前答案
这里可以直接break 会更快一点

用户头像
努力挣钱   2021-10-21 16:34         踩      回复

而且评论里 的那个数据 不会被卡

用户头像
义往尘沙   2021-06-03 17:16         踩      回复

y总数据没卡死，你的最终代码把你之前的dfs替换上之后过不了这个数据
4 8
78 64 38 84
73 36 10 39
48 45 97 24
92 25 46 44
27 37 9 9
52 35 3 83
33 94 71 39
63 95 24 97
会tle

用户头像
义往尘沙   2021-06-03 17:16         踩      回复

但是交的话会ac，总而言之，y总nb！

用户头像
KaMtuo   2021-06-03 20:25         踩      回复

确实t了，不过手写哈希可以卡过去，大概就是y总代码比我快了个常数，手写哈希又比unordered_set快了个常数吧hh，谢谢指出！

用户头像
Biang   2021-04-04 16:40         踩      回复

tql tql

用户头像
今天小胡网抑了嘛   2021-03-23 19:35         踩      回复

蓝桥的没有判断连通性

用户头像
KaMtuo   2021-03-25 10:07         踩      回复

是的

用户头像
doubleSix   2021-02-22 21:42         踩      回复

蓝桥杯ac代码有误，数据如下：
4 3
10 10 10 10
8 13 5 10
4 23 7 10

用户头像
KaMtuo   2021-02-23 12:06         踩      回复

蓝桥杯AC代码意思是在蓝桥杯官网可以AC，并不是说完全正确，蓝桥杯官网的数据并没有考虑分割两部分连通。这部分缺陷在算法2都进行了完善。

用户头像
KaMtuo   2021-02-23 12:09      1    踩      回复

你的测试数据用该代码跑出来包含左上角分割区域是｛10，10，13，23，4｝，剩余部分是不连通的，确实是错误答案，但蓝桥杯没考虑这种情况，依旧可以AC。

用户头像
KaMtuo   2021-02-23 12:11      1    踩      回复

感谢质疑

用户头像
doubleSix   2021-02-23 22:01    回复了 KaMtuo 的评论         踩      回复

仔细看了下你的题解，写的太好了，感谢！