题目描述

You are given a doubly linked list which in addition to the next and previous pointers, it could have a child pointer, which may or may not point to a separate doubly linked list. These child lists may have one or more children of their own, and so on, to produce a multilevel data structure, as shown in the example below.

Flatten the list so that all the nodes appear in a single-level, doubly linked list. You are given the head of the first level of the list.

样例

Input:
 1---2---3---4---5---6--NULL
         |
         7---8---9---10--NULL
             |
             11--12--NULL

Output:
1-2-3-7-8-11-12-9-10-4-5-6-NULL

Explanation for the above example:

Given the following multilevel doubly linked list:

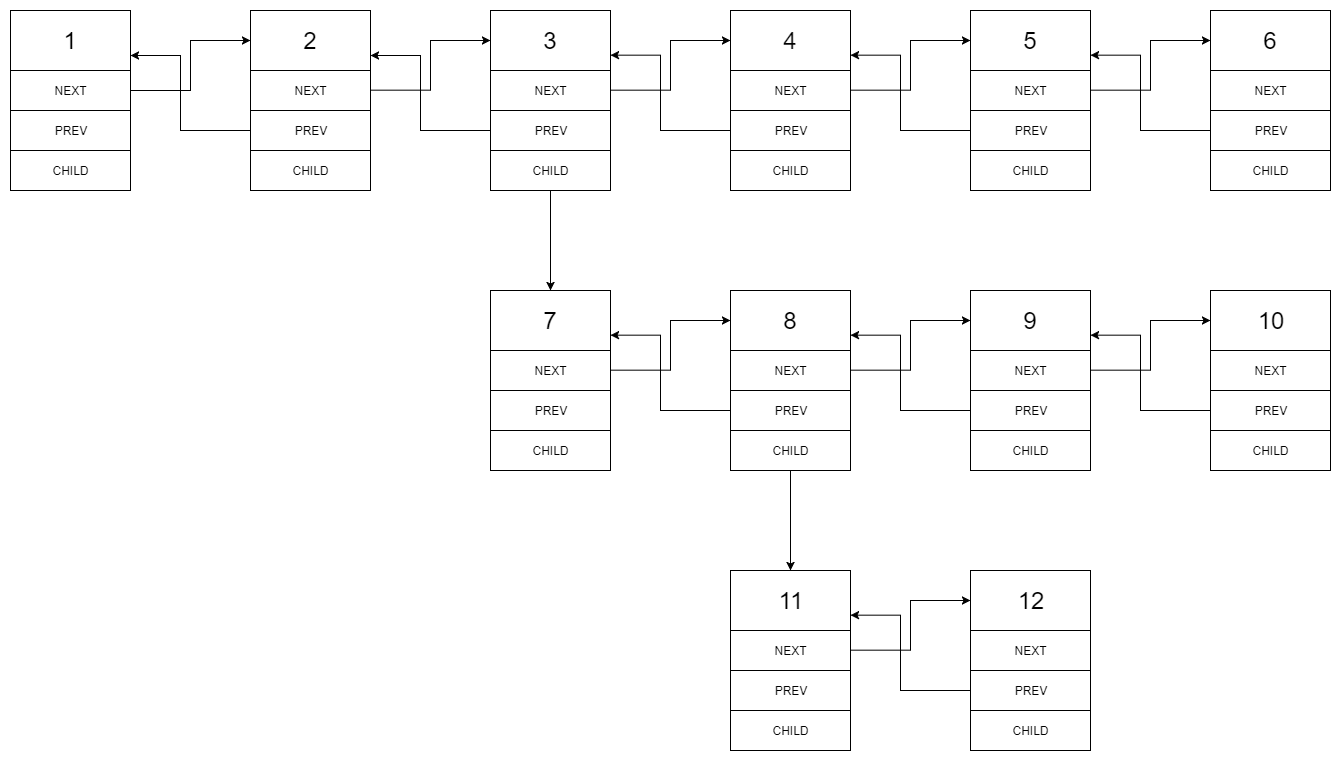
We should return the following flattened doubly linked list:

题意：给一个带有孩子节点的多层双向链表，希望将这个链表扁平化变成一个单层的双向链表。

算法1

(递归解法)

题解：类似于树一样的结构，使得我们考虑用递归处理这样的问题。对于每一个节点总共有四种情况，只有后驱节点；只有孩子节点；即没有孩子节点也没有后驱节点；有后驱节点和孩子节点。其实本质上这一题也是个链表插入的问题。

当我们遇到一个有孩子节点的节点时，如果我们有一个函数能获得该孩子节点的扁平化后的末尾节点（如遍历到3号节点时，如果我们已经将其孩子链表变成了7-8-11-12-9-10，而且我们得到了末尾10号节点），那么我们只需要将7-8-11-12-9-10这一段链表插入到3-4之间就可以得到答案了。

C++ 代码

    Node* flatten(Node* head) {
        Node *p = flat(head);
        return head;
    }
    Node* flat(Node* head)
    {
        while(head)
        {
        //既没有孩子节点也没有后驱节点，说明已经是该层最后一个节点了，如6,10,12。
            if(!head->next && !head->child)return head;
        //如果没有孩子节点，只有后驱节点。如1，2，4，5，7，9，11
            if(!head->child) 
                head = head->next;
        //既有孩子节点也有后驱节点
            else if(head->next)
            {
          //先将孩子链表扁平化并返回末尾节点。
                Node* tail = flat(head->child);
                Node* temp = head->next;
                tail->next = temp;
                head->next = head->child;
          //将扁平化的链表插入当前节点的后面，注意是双向链表，并且孩子节点需要变成NULL
                if(tail->next)tail->next->prev = tail;
                if(head->next)head->next->prev = head;
                head->child = NULL;
          //更新当前节点
                head = tail->next;
            }else
            {   //只有孩子节点，没有后驱节点。那么只需要将孩子节点变成后驱节点就可以了
                head->next = head->child;
          head->next->prev = head;
                head->child = NULL;
                head = head->next;
            }
        }
        return head;
    }