题目大意：

一棵有 N 个点的树，选择一条边将其权值变为0，求出所给出 M 条路径中最大值的最小值

题意分析：

对于一种情况，M 条路径中的最大值已经确定了，那么关键在于零边的选择，也就是说，要存在这么一条零边，使得 M 条路径中的最大值尽量小，同时零边选择之后的最大值也要尽量小。

但由于这个小的定义很模糊，需要我们给出一个目标值，于是我们选择 二分答案 ，每次要让路径的权值和大于 mid 的所有路径，在减去一条公共边后，权值和全部小于等于 mid ，mid其实就是我们的目标值。

而要使所有权值和大于 mid 的路径在减去一条公共边后权值和小于等于 mid ，等价于让选择零边前，权值和大于 mid 的路径中权值和最大的路径满足上述条件。

于是我们的目标就已经很明确了：
1） 预处理好 M 条路径的权值和
2） 想办法实现记录每条边被 权值和大于目标值的路径 覆盖的次数
3） 判断目标值是否符合条件

明确算法

1）预处理 M 条路径权值和可以用一个 lca 的扩张应用：
在树中，两点间距离等于它们到固定点距离的和减去固定点到它们最近公共祖先的距离的两倍
可以用图表示，很好理解：

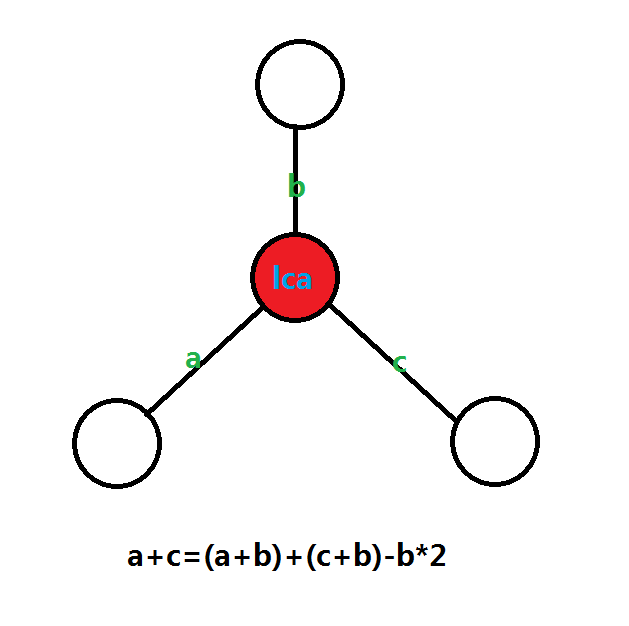
我们选择根节点作为固定点，因为它是所有点的祖先
2） 实现记录每条边的覆盖次数可以用树上差分，就是 lca 减 2 ，两子节点各加 1
这样之后再从叶子节点往上累加求得前缀和，就是每条边的覆盖次数

代码实现：

#include<bits/stdc++.h>
using namespace std;

const int N=300000+10;

struct node
{
    int u,v,dis,far;
}path[N];
int lson[N],maxlen[N],fa[N],dep[N],top[N],dif[N],dist[N];
int head[N],ver[N*2],nex[N*2],edge[N*2],num[N];
int tot=0,n,m,l=0,r=0,mid,sum=0;

void add(int x,int y,int z)
{
    ver[++tot]=y;
    nex[tot]=head[x];
    head[x]=tot;
    edge[tot]=z;
}

void dfs1(int x)
{
    dif[++sum]=x;
    //预处理出搜索序，后面有用 
    dep[x]=dep[fa[x]]+1;
    maxlen[x]=dep[x];
    for(int i=head[x];i;i=nex[i])
    {
        int y=ver[i];
        if(y!=fa[x])
        {
            fa[y]=x;
            dist[y]=dist[x]+edge[i];
            dfs1(y);
            maxlen[x]=max(maxlen[y],maxlen[x]);
            if(maxlen[y]>maxlen[lson[x]]) lson[x]=y;
        }
    }
}

void dfs2(int x,int nowtop)
{
    top[x]=nowtop;
    if(lson[x]) dfs2(lson[x],nowtop);
    for(int i=head[x];i;i=nex[i])
    {
        int y=ver[i];
        if(y!=fa[x]&&y!=lson[x]) dfs2(y,y);
    }
}

//树链剖分求解 lca 用两次 dfs 预处理 ，预处理时顺带把点到根节点的距离 dist 处理出来 

int lca(int x,int y)
{
    while(top[x]!=top[y])
    {
        if(dep[top[x]]<dep[top[y]]) swap(x,y);
        x=fa[top[x]];
    }
    return dep[x]<dep[y]?x:y;
}

void prework()
{
    //预处理出 M 条路径的权值和 
    for(int i=1,x,y,z;i<=m;i++)
    {
        x=path[i].u,y=path[i].v;
        z=path[i].far=lca(x,y);     //顺带记录 lca 后面有用 
        path[i].dis=dist[x]+dist[y]-2*dist[z];
    }
}

bool check(int mid)
{
    memset(num,0,sizeof(num));
    int cnt=0,maxx=0;
    for(int i=1;i<=m;i++)
        if(path[i].dis>mid)
        {
            cnt++;
            num[path[i].u]++;
            num[path[i].v]++;
            num[path[i].far]-=2;
            //树上差分 
            maxx=max(maxx,path[i].dis);
            //记录权值和大于目标值的路径 
        }
    if(cnt==0) return true;
    for(int i=n;i>=1;--i)
        num[fa[dif[i]]]+=num[dif[i]];
    //从叶子节点累加 ，只需把搜索序倒过来 
    for(int i=2;i<=n;i++)
        if(num[i]==cnt&&mid+dist[i]-dist[fa[i]]>=maxx) return true;
    //要满足两个条件：这条边覆盖权值和大于目标值的所有路径，并使这些路径在减去该边权值后不大于目标值 
    return false;
}

int main()
{

    scanf("%d%d",&n,&m);

    for(int i=1,x,y,z;i<n;i++)
    {
        scanf("%d%d%d",&x,&y,&z);
        add(x,y,z);
        add(y,x,z);
        r+=z;
    }

    for(int i=1;i<=m;i++) scanf("%d%d",&path[i].u,&path[i].v);

    dfs1(1);
    dfs2(1,1);
    prework();
    //预处理~~ 

    while(l<r)
    {
        mid=(l+r)>>1;
        if(check(mid)) r=mid;
        else l=mid+1;
    }

    printf("%d",l);

    return 0;
}

关于树链剖分，其实有更多的用处
戳这里–> https://www.acwing.com/blog/content/350/