题目描述

Given a linked list, return the node where the cycle begins. If there is no cycle, return null.

To represent a cycle in the given linked list, we use an integer pos which represents the position (0-indexed) in the linked list where tail connects to. If pos is -1, then there is no cycle in the linked list.

Note: Do not modify the linked list.

题意：给一个链表，判断这个链表是否有环，如果有环，返回环的入口节点。

算法1

题解：使用快慢指针，快指针每次走两格，慢指针每次走一格，当两个指针第一次相遇的时候，将慢指针返回起始点，然后快慢指针每次走一格，再次相遇就是环的入口节点。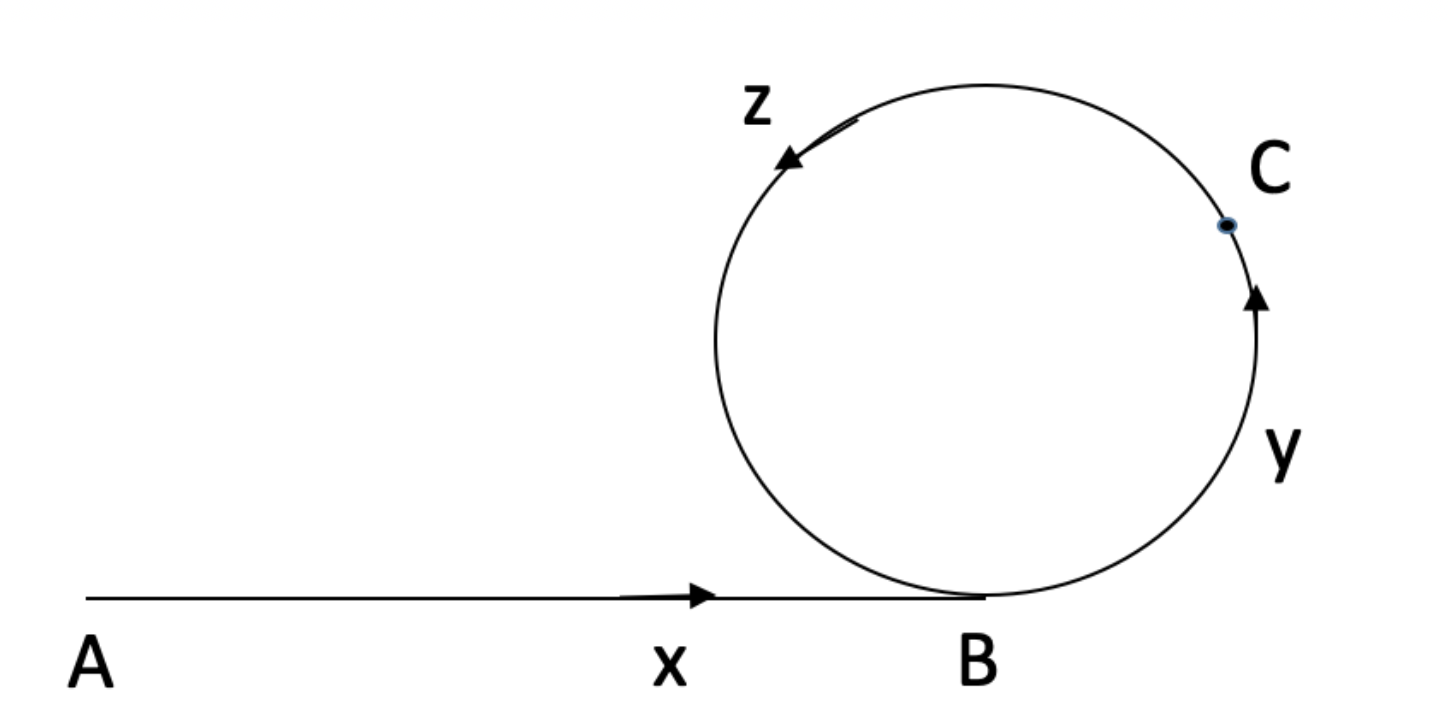

证明：这里使用的是类似@yxc的讲解图。假设A是链表起点，B是链表环的入口，C是二者第一次相遇的地方。AB，BC，CB的距离分别为$x,y,z$，那么环的长度就是$y+z$二者第一次相遇时，可以知道二者分别走过的距离是：

$slow:x+y+k_1(y+z)$

$quick:x+y+k_2(y+z)$

因为快节点走过的距离是慢节点的两倍：$2(x+y+k_1(y+z))=x+y+k_2(y+z)$

可以得到$x+y=(k_2-k_1)(y+z)$

进一步得到$x=(k_2-k_1-1)(y+z)+z$

也就是说AB之间的距离是整数倍个环长度加上CB的长度。那么如果两个节点分别在A，C两点开始走，一个节点从A走到B$dist = x$，另一个节点必然也会同时到达B，$dist = (k_2-k_1-1)(y+z)+z$。

C++ 代码

    ListNode *detectCycle(ListNode *head) {
        if(!head || !head->next) return NULL;
        ListNode* slow = head;
        ListNode* quick = head;
        while(quick && quick->next)
        {
            slow = slow->next;
            quick = quick->next->next;
            if(slow == quick)
            {
                slow = head;
                while(slow !=quick)
                {
                    slow = slow->next;
                    quick = quick->next;
                }
                return slow;
            }
        }
        return NULL;
    }