题目描述

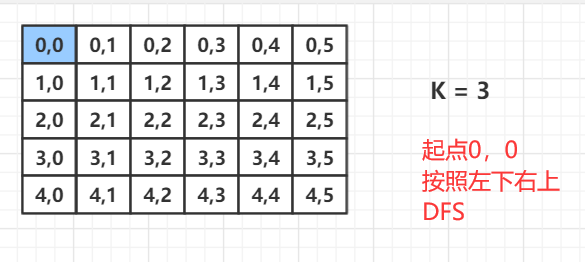
地上有一个 m 行和 n 列的方格，横纵坐标范围分别是 0∼m−1 和 0∼n−1。

一个机器人从坐标0,0的格子开始移动，每一次只能向左，右，上，下四个方向移动一格。

但是不能进入行坐标和列坐标的数位之和大于 k 的格子。

请问该机器人能够达到多少个格子？

样例

输入：k=7, m=4, n=5

输出：20

输入：k=18, m=40, n=40

输出：1484

解释：当k为18时，机器人能够进入方格（35,37），因为3+5+3+7 = 18。
      但是，它不能进入方格（35,38），因为3+5+3+8 = 19。

注意:

0<=m<=50
0<=n<=50
0<=k<=100

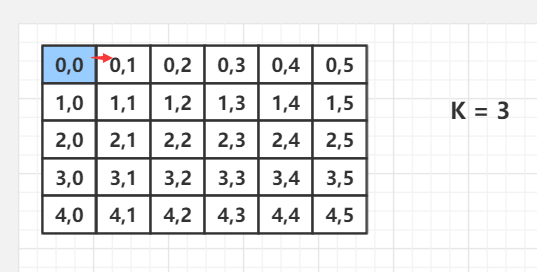
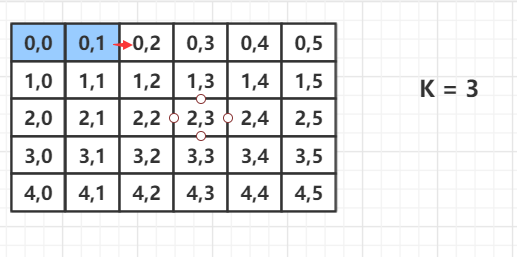
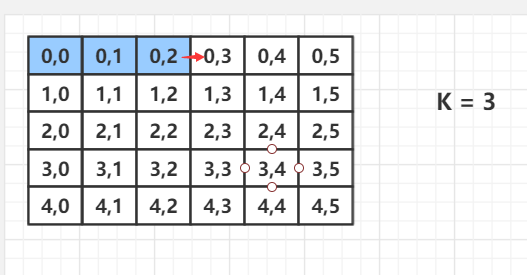
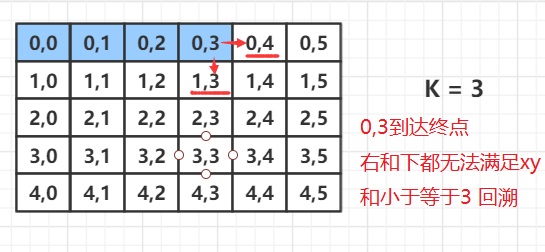
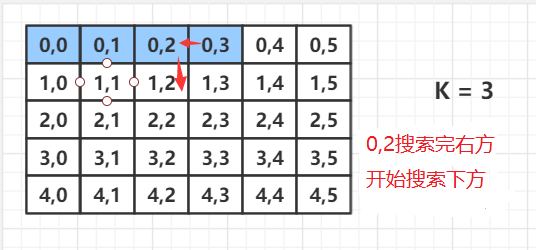
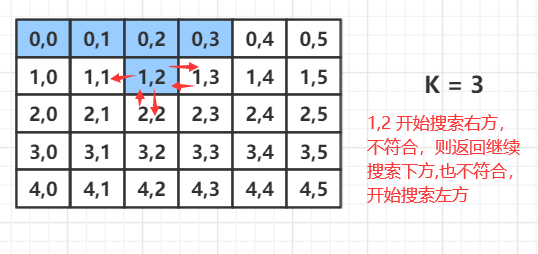
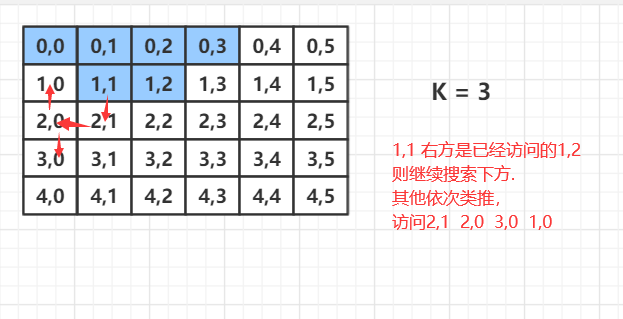
算法1

x y的+- 1 的搜索模板
在添加上检测每个格子是否符合要求的代码
与递归回溯搜索代码结合

C++ 代码

class Solution {
public:
    vector<vector<bool>> vis;
    int count = 0;
    bool Check(int x, int y, int rows, int cols, int limit) {

        if (x <0 || y < 0 || x > rows - 1 || y > cols - 1)
            return false;

        int sum = 0;
        while (x != 0) {
            sum += x % 10;
            x = x / 10;
            if (sum > limit)
                return false;
        }

        while (y != 0) {
            sum += y % 10;
            y = y / 10;
            if (sum > limit)
                return false;
        }

        return true;
    }

    void dfs(int x, int y, int rows, int cols, int limit)
    {
        //坐标位置不对 或者已经访问过 即可返回
        if (x <0 || y < 0 || x > rows - 1 || y > cols - 1 || vis[x][y])
            return;
        //标记是否访问 然后检查该坐标是否符合要求 计数是否加1
        if (vis[x][y] == false) {
            vis[x][y] = true;
            if (Check(x, y, rows, cols, limit) == true) {
                count++;
            }
            else {
                return;
            }
        }

        //本坐标符合要求 则进行上下左右的扩展
        dfs(x + 1, y, rows, cols, limit);
        dfs(x - 1, y, rows, cols, limit);
        dfs(x, y + 1, rows, cols, limit);
        dfs(x, y - 1, rows, cols, limit);


    }




    int movingCount(int threshold, int rows, int cols)
    {
        int x = 0, y = 0;  count = 0;
        //创建标注是否搜索到的标记数组
        vis = vector<vector<bool>>(rows, vector<bool>(cols, false));
        //开始 递归回溯搜索
        dfs(0, 0, rows, cols, threshold);

        return count;
    }
};

算法1

BFS

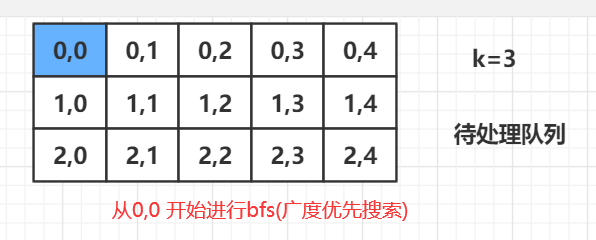
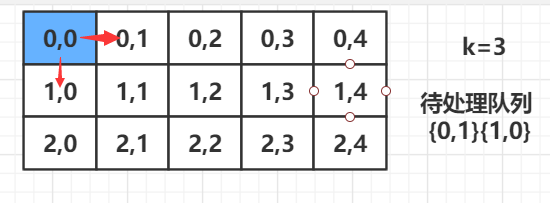
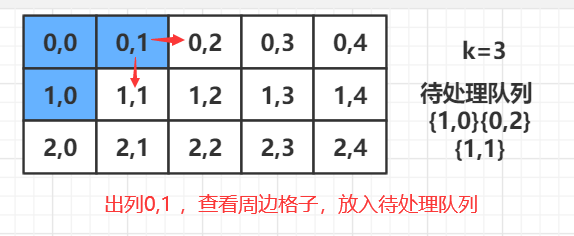
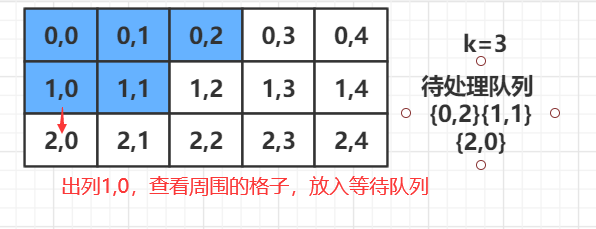
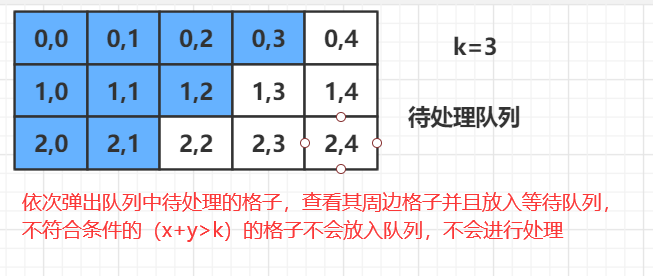
C++ 代码

class Solution {
public:
    queue<pair<int,int>> q;
    int addx[4] = {1,-1,0,0};
    int addy[4] = {0,0,1,-1};
    vector<vector<int>> vis;
    int ans;

    int Sumxy(int a){
        int ret = 0;
        while(a!=0){
            ret += a%10;
            a=a/10;
        }
        return ret;
    }

    int movingCount(int m, int n, int k) {
        q.push({0,0});
        vis = vector<vector<int>>(m,vector<int>(n));
        vis[0][0]= 1;

        while(!q.empty()){
            pair<int,int> XY = q.front();q.pop();
            if(Sumxy(XY.first)+Sumxy(XY.second) >k) continue;
            ans++; 
            for(int i = 0;i < 4;i++){
                int newx = XY.first+addx[i];
                int newy = XY.second+addy[i];

                if(newx>=0 && newx<m && newy>=0 && newy<n && 0 == vis[newx][newy]){
                    vis[newx][newy] = 1;
                    q.push({newx,newy});
                }
            }
        }

        return ans;
    }
};