题目描述

Given a non-empty 2D matrix matrix and an integer k, find the max sum of a rectangle in the matrix such that its sum is no larger than k.

Example:

Input: matrix = [[1,0,1],[0,-2,3]], k = 2
Output: 2
Explanation: Because the sum of rectangle [[0, 1], [-2, 3]] is 2,
and 2 is the max number no larger than k (k = 2).
Note:

The rectangle inside the matrix must have an area > 0.
What if the number of rows is much larger than the number of columns?
题意：求二维数组中，子数组和不大于K的最大值。

算法1

(暴力枚举) $O(n^2*m^2)$

首先暴力解法就是遍历上下左右四条边，使用前缀和进行求解即可，这样的话时间复杂度为$O(n^2m^2)$。

算法2

前缀和+枚举+二分 $O(m^2*nlogn)$

• 我们先考虑另一个问题，在一维数组求子数组的最大值，对于这样的问题，我们可以在$O(n)$的时间复杂度内求解：$dp[i]$代表以第$i$个元素结尾的子数组最大和，那么答案就是$max(dp[i])$，其中状态转移方程如下：

$$dp[i] = (dp[i - 1] \leq 0)?A[i]:(dp[i - 1]+A[i])$$

• 那么我们再来考虑一个问题，在一维数组求和不超过K的最大子数组的和，我们可以在$O(nlogn)$的时间复杂度内求解。我们知道可以使用前缀和求解子区间和：$sum(A[i:j]) = preSum[j] - preSum[i - 1]$。那么对于每一个$preSum[j]$，我们可以将遇到过的前缀后存入一个set中，再从set中找到一个大于等于$preSum[j] - k$的最小值，这样他们的差值就是小于等于$k$的最大值。这种查找的时间复杂度是$logn$的，总共需要查找$n$次，所以总共的时间复杂度为$O(nlogn)$。

回到我们这个问题，我们可以先使用

1. 预先处理每一行行内的前缀和，时间复杂度$O(n*m)$。
2. 二重循环遍历矩形的左边$l$和右边$r$，时间复杂度$O(m^2)$。
3. 求出每一行$[l,r]$的子区间和，时间复杂度$O(n)$，将问题转化成一维数组中不超过$k$的最大子数组的和。
4. 求解矩形左右边分别为$[l,r]$时，一维数组中不超过$k$的最大子数组的和时间复杂度$O(nlogn)$。

总的时间复杂度$O(m^2nlogn)$，如果$m>n$，就枚举上下边，预处理列的前缀和。

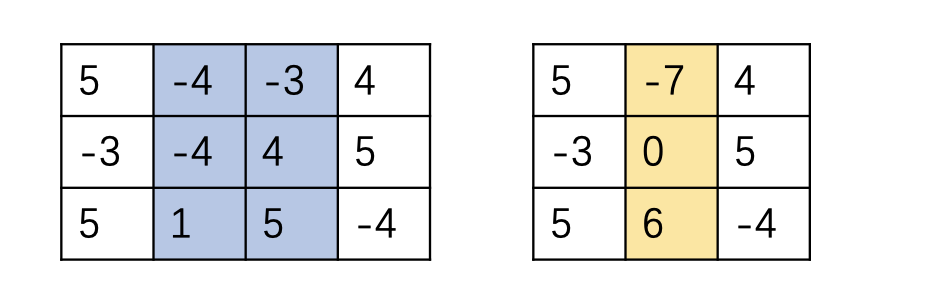
假设$l = 1,r=2$(遍历所有的$l,r$，时间复杂度$O(m^2)$)，问题转化成求$[-7,0,6]$中不超过$k$的最大连续子数组$O(nlogn)$ 。

C++ 代码

    int maxSumSubmatrix(vector<vector<int>>& matrix, int k) {
        int n = matrix.size(),m = matrix[0].size();
        int res = INT_MIN;
        int s[n + 1][m + 1];
        memset(s,0,(n + 1)*(m + 1)*sizeof(int));
        for(int i = 0 ; i < n ; i ++)
            for(int j = 0 ; j < m ; j++)
                s[i][j + 1] = s[i][j] + matrix[i][j];    
        //枚举矩形的左右边界
        for(int i = 0 ; i < m ; i ++)
        {
            for(int j = i ; j < m ; j ++)
            {
                //myset存储的是遇到过的前缀和
                //A存储的是每一行第i列到第j的和(二维数组一维化)
                //temp是当前前缀和
                set<int> myset;
                int A[n],temp = 0;
                myset.insert(0);
                //  求解一维数组不超过k的前缀和。
                for(int t = 0 ; t < n ; t ++){
                    A[t] = s[t][j + 1] - s[t][i];
                    temp += A[t]; 
                    auto it = myset.lower_bound(temp - k);
                    if(it!=myset.end())
                        res = max(res,temp - *it);
                    myset.insert(temp);
                }
            }
        }    
        return res;
    }