题目描述

在平面上给定两个矩形，请计算它们覆盖区域（并集）的面积。

每个矩形给出左下角和右上角坐标，如下所示：

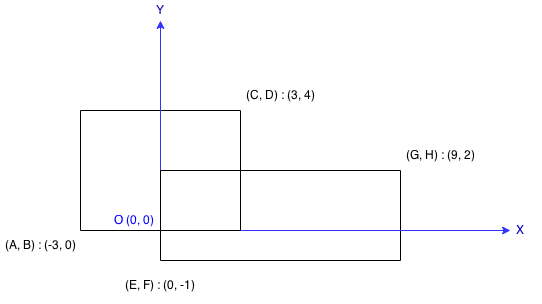
注意： 总面积不会超出int范围。

样例

输入：A = -3, B = 0, C = 3, D = 4, E = 0, F = -1, G = 9, H = 2
输出：45

算法

(计算几何) $O(1)$

两个矩形并集的面积 = 两个矩形的总面积 - 两个矩形交集的面积。

两个矩形如果有交集，那么交集一定是矩形，剩下的问题是求出交集的长和宽。

求交集的长和宽是一个一维问题，即在数轴上给出线段 $[A, B]$ 和 $[C, D]$，求它们交集的长度。
其交集的长度：$L = min(B, D) - max(A, C)$，如果 $L \lt 0$，说明两个线段不重合。

注意：

1. 虽然总面积不会超出int范围，但中间计算结果可能会溢出int，所以中间结果要用long long存储。比如两条线段分别在 [INT_MIN, INT_MIN+1] 和 [INT_MAX-1, INT_MAX]，虽然它们不重合，但 min(INT_MAX, INT_MIN+1) - max(INT_MIN, INT_MAX-1) 会溢出int。
2. 另外这道题目的数据比较强，两个矩形面积的和可能会超出int范围，所以我们要把返回值中的减法提前。

时间复杂度分析：只有常数次计算，所以时间复杂度是 $O(1)$。

C++ 代码

class Solution {
public:
    int computeArea(int A, int B, int C, int D, int E, int F, int G, int H) {
        long long X = min(C, G) + 0ll - max(A, E);
        long long Y = min(D, H) + 0ll - max(B, F);
        return (C - A) * (D - B) - max(0ll, X) * max(0ll, Y) + (G - E) * (H - F);
    }
};