算法

(搜索) $O(2^n)$

首先简化题意：将所有节点按到根节点的距离分层，然后从每层中选择一个节点，删掉以该节点为根的子树。问最后剩下的节点个数最少是多少？

由于这道题目的数据较弱，且贪心算法均有反例，因此直接暴搜出所有切割方案，保留最小值即可。

首先预处理出每一层的节点集合，以及每棵子树的大小。

然后从第一层开始，依次枚举每一层中删除哪棵子树，枚举之后通过深度优先遍历，将整棵子树中的边全部标记为不可选，再递归到下一层继续枚举。递归结束时需要再次深度优先遍历整棵子树，将每条边的状态恢复为可选。

当枚举到最后一层时，更新最小值。

暴力枚举过程中需要维护当前已经删除的节点总数。

时间复杂度

构造如下图所示的一棵包含 $n$ 个节点的树：

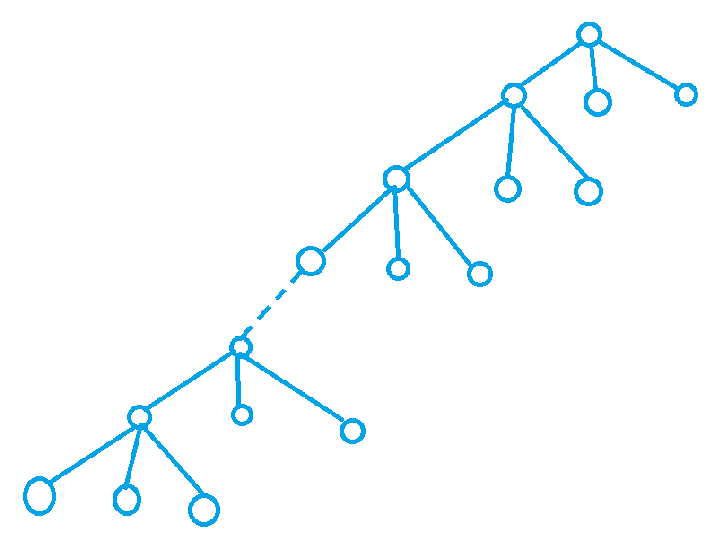
则总共有 $\frac{n - 1}{3}$ 层，每层至少有两种选择，因此暴力枚举的计算量至少是 $2^{\frac{n - 1}{3}}$。

因此最坏情况下的时间复杂度是 $O(2^n)$。

C++ 代码

#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

const int N = 310, M = N * 2;

int n, m;
int h[N], e[M], ne[M], idx;
vector<int> level[N];
int c[M], cnt[N];
int ans = N;

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

int dfs_level(int u, int depth, int father)
{
    cnt[u] = 1;

    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (j == father) continue;
        cnt[u] += dfs_level(j, depth + 1, u);
        level[depth].push_back(i);
    }

    return cnt[u];
}

void dfs_draw(int j, int color)
{
    c[j] = color;
    for (int i = h[e[j]]; ~i; i = ne[i])
        if (i != (j ^ 1))   // i不是j的反向边
            dfs_draw(i, color);
}

void dfs(int u, int s)
{
    ans = min(ans, s);

    for (int i = 0; i < level[u].size(); i ++ )
    {
        int j = level[u][i];
        if (!c[j])
        {
            dfs_draw(j, 1);
            dfs(u + 1, s - cnt[e[j]]);
            dfs_draw(j, 0);
        }
    }
}

int main()
{
    cin >> n >> m;

    memset(h, -1, sizeof h);
    for (int i = 0; i < m; i ++ )
    {
        int a, b;
        cin >> a >> b;
        add(a, b), add(b, a);
    }

    dfs_level(1, 0, -1);
    dfs(0, n);

    cout << ans << endl;

    return 0;
}