题意：什么是树的重心？

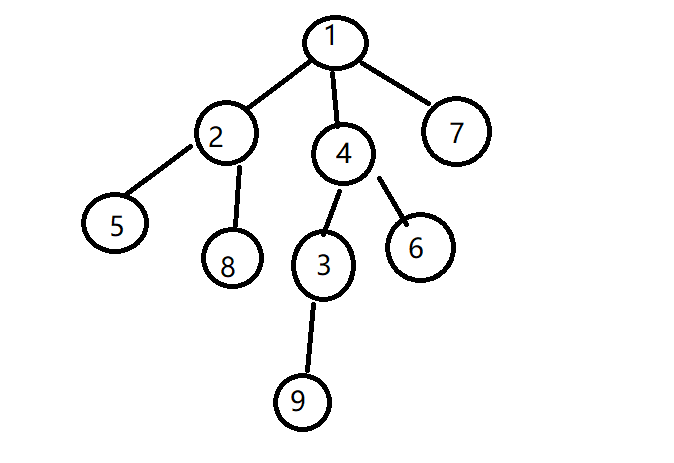
树的重心是指，删除某个结点后剩下的最大连通子树的结点数目最小，如下图是根据样列生成的树，若删除结点1，则剩下三个子树最大的是中间那颗结点有4个，即剩下的最大连通子树的结点数目为4；若删除结点2，则剩下两个数目为1的子树和一个数目为6的子树，即剩下的最大连通子树的结点数目为6；若删除结点3，剩下一个数目为1的子树，和一个数目为7的子树，即剩下的最大连通子树的结点数目为7……枚举可得剩下的最小的最大连通子树的结点数目为4也就是说结点1是树的重心。另外注意题目要求答案是输出剩下的最小的最大连通子树的结点数目。

思路

深搜，算出每个结点被删除后剩下的最大连通子树的结点数目，输出最小值即可，那么问题就是怎么求一个结点被删除后的最大连通子树的结点数目，删除一个结点后，剩下的子树可以被分为两个部分，例如删除结点4：

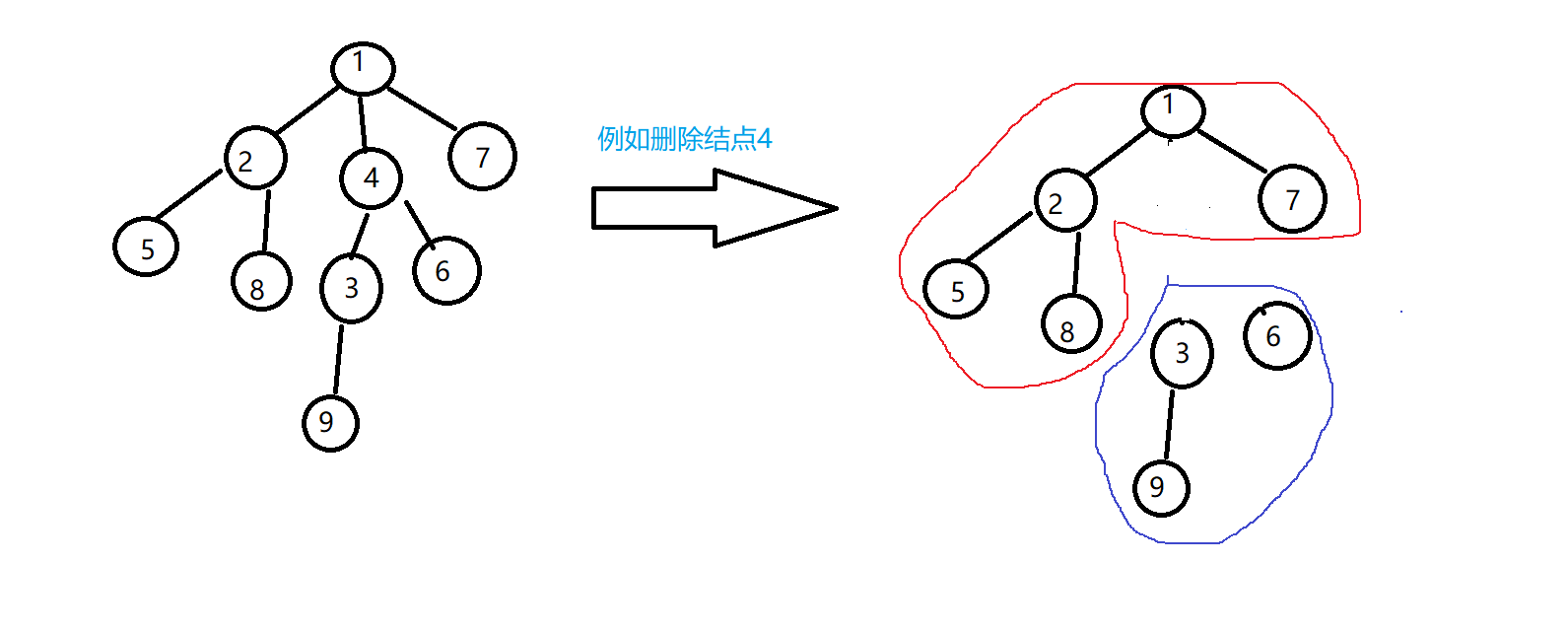
蓝色部分是结点4的子树，红色部分我们暂时称为其他部门，因为我们知道树的总结点数n，只要能算出蓝色部分的数目s，那么其他部分的数目就是n-s。

怎么写代码

代码怎么写有两个问题，一是这颗树我们要怎么存储，二是上述dfs怎么实现
首先树是一种特殊的图（无向图），存储图有邻接矩阵法和邻接表法，这里选择邻接表法，另外这里的是无向图，所以存边的时候要存正反两条。

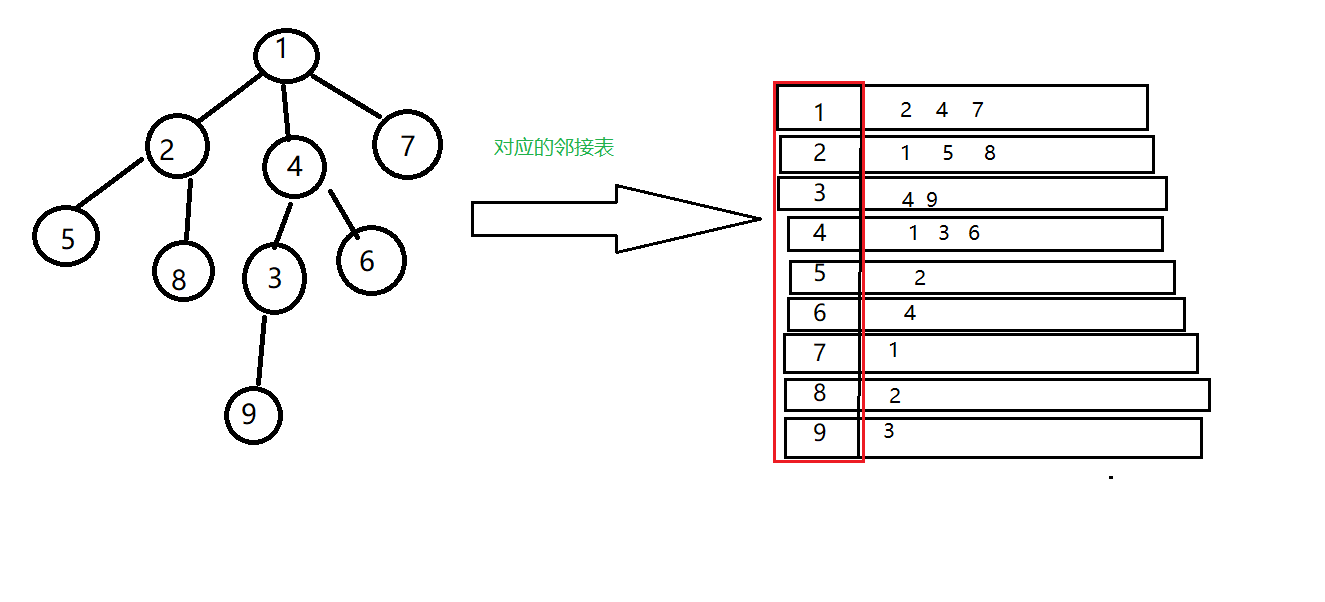
存树的代码

    Scanner scanner = new Scanner(System.in);
    int n = scanner.nextInt();
    Object[] tree = new Object[n + 1];  //用于存树的邻接表，我用的数组，也可以用Map<Integer,List<Integer>>
    boolean[] state = new boolean[n + 1];  //用于判断结点i是否被访问过，下标从1开始

    for (int i = 0; i < n - 1; i++) {
        int a = scanner.nextInt(), b = scanner.nextInt();
        if (tree[a] == null) {
            List<Integer> list = new LinkedList<>();
            list.add(b);
            tree[a] = list;
        } else {
            List<Integer> list = (List<Integer>) tree[a];
            list.add(b);
        }
        //边是无向的，所以需要反着再添加一次
        if (tree[b] == null) {
            List<Integer> list = new LinkedList<>();
            list.add(a);
            tree[b] = list;
        } else {
            List<Integer> list = (List<Integer>) tree[b];
            list.add(a);
        }

    }

这样效果如下：

最后是dfs怎么实现，我们只要在深搜的时候统计当前结点子树的个数，然后判断出最小的最大连通子树结点数目。

java代码

import java.util.LinkedList;
import java.util.List;
import java.util.Scanner;

public class Main {

    static int ans; //最终答案

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        ans = n + 1;
        Object[] tree = new Object[n + 1];
        boolean[] state = new boolean[n + 1];
        //构造树
        for (int i = 0; i < n - 1; i++) {
            int a = scanner.nextInt(), b = scanner.nextInt();
            if (tree[a] == null) {
                List<Integer> list = new LinkedList<>();
                list.add(b);
                tree[a] = list;
            } else {
                List<Integer> list = (List<Integer>) tree[a];
                list.add(b);
            }
            //边是无向的，所以需要添加两条边
            if (tree[b] == null) {
                List<Integer> list = new LinkedList<>();
                list.add(a);
                tree[b] = list;
            } else {
                List<Integer> list = (List<Integer>) tree[b];
                list.add(a);
            }

        }
        dfs(1, n, tree, state);
        System.out.println(ans);
        scanner.close();
    }

    // 返回以u为根的子树的大小
    private static int dfs(int u, int n, Object[] tree, boolean[] state) {
        state[u] = true;
        List<Integer> list = (List<Integer>) tree[u];
        if (list == null)
            return 1;
        int cont = 1; // 统计当前节点子树所有的节点
        int res = 0;// 统计最大连通块大小
        for (int i : list) {
            if (!state[i]) {
                int child = dfs(i, n, tree, state); //一颗子树的结点数目
                res = Math.max(res, child);  //保证res中存的是最大的那颗子树结点数目
                cont += child;
            }
        }
        res = Math.max(res, n - cont); //看看是上图二中红色部分大还是蓝色部分大
        ans = Math.min(ans, res);
        return cont;
    }

}