题目描述

某国的军队由 N 个部门组成，为了提高安全性，部门之间建立了 M 条通路，每条通路只能单向传递信息，即一条从部门 a 到部门 b 的通路只能由 a 向 b 传递信息。

信息可以通过中转的方式进行传递，即如果 a 能将信息传递到 b，b 又能将信息传递到 c，则 a 能将信息传递到 c。

一条信息可能通过多次中转最终到达目的地。

由于保密工作做得很好，并不是所有部门之间都互相知道彼此的存在。

只有当两个部门之间可以直接或间接传递信息时，他们才彼此知道对方的存在。

部门之间不会把自己知道哪些部门告诉其他部门。

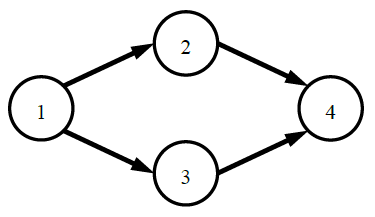
上图中给了一个 4 个部门的例子，图中的单向边表示通路。

部门 1 可以将消息发送给所有部门，部门 4 可以接收所有部门的消息，所以部门 1 和部门 4 知道所有其他部门的存在。

部门 2 和部门 3 之间没有任何方式可以发送消息，所以部门 2 和部门 3 互相不知道彼此的存在。

现在请问，有多少个部门知道所有 N 个部门的存在。

或者说，有多少个部门所知道的部门数量（包括自己）正好是 N。

输入样例

4 4
1 2
1 3
2 4
3 4

输出样例

2

C++ 代码(bfs)

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;

const int N=1001,M=10001;
int h1[M],e1[M],ne1[M],idx1;    //向后链表
int h2[M],e2[M],ne2[M],idx2;    //向前链表
int n,m,ans;
bool vis[N][3]; //有可能产生环，点i可能在点j的遍历中当一个中转站
                //经过这个中转站的方向可能不同
                //所以分开标记路过点i的方向vis[i][0...1]
                //和是否遍历过vis[i][2]

inline void add1(int a,int b)   //加入向后链表
{
    e1[idx1]=b,ne1[idx1]=h1[a],h1[a]=idx1++;
}

inline void add2(int a,int b)   //加入向前链表
{
    e2[idx2]=b,ne2[idx2]=h2[a],h2[a]=idx2++;
}

inline void bfs(int u)
{
    memset(vis,0,sizeof vis);
    queue<int> chain;

    //标记自身
    int cnt=1;
    vis[u][2]=1;

    /******向后遍历******/
    chain.push(u);
    while(!chain.empty())
    {
        int p=chain.front();    chain.pop();
        for(int i=h1[p];~i;i=ne1[i])
        {
            int j=e1[i];
            if(vis[j][0]) continue; //已经向后遍历过了，有请下一位选手！
            vis[j][0]=1;
            if(!vis[j][2])  //遍历过没？(不分方向)
            {
                vis[j][2]=1;
                cnt++;
            }
            chain.push(j);
        }
    }

    /******向前遍历******/
    chain.push(u);  //由于chain已经清空，直接再加入即可
    while(!chain.empty())
    {
        int p=chain.front();    chain.pop();
        for(int i=h2[p];~i;i=ne2[i])
        {
            int j=e2[i];
            if(vis[j][1]) continue; //已经向前遍历过了，有请下一位选手！
            vis[j][1]=1;
            if(!vis[j][2])  //遍历过没？(不分方向)
            {
                vis[j][2]=1;
                cnt++;
            }
            chain.push(j);
        }
    }
    if(cnt==n)
        ans++;  //找到了！喜大普奔，ans++
    return;
}

int main()
{
    //初始化
    memset(h1,-1,sizeof h1);
    memset(h2,-1,sizeof h2);

    cin>>n>>m;
    while(m--)
    {
        int a,b;
        scanf("%d %d",&a,&b);
        add1(a,b);add2(b,a);    //两次方向不一样
    }
    for(int i=1;i<=n;i++)
        bfs(i);
    cout<<ans<<endl;
    return 0;
}