题目描述

有两位玩家参与了一场在二叉树上进行的回合制游戏。游戏中，给出二叉树的根结点 root，树上总共有 n 个结点，且 n 为奇数，其中每个结点上的值从 1 到 n 各不相同。

最开始时，一号玩家取一个值 x 满足 1 <= x <= n，二号玩家也取一个值 y 满足 1 <= y <= n 且 y != x。
一号玩家给值为 x 的结点染上红色，而二号玩家给值为 y 的结点染上蓝色。

之后两位玩家轮流进行操作，每一回合，玩家选择一个他之前涂好颜色结结点，将所选结点一个 未着色 的邻结点（即左右子结点、或父结点）进行染色。

如果当前玩家无法找到这样的结点来染色时，他的回合就会被跳过。

若两个玩家都没有可以染色的结点时，游戏结束。着色结点最多的那位玩家获得胜利️。

现在，假设你是二号玩家，根据所给出的输入，假如存在一个 y 值可以确保你赢得这场游戏，则返回 true；若无法获胜，就请返回 false。

样例

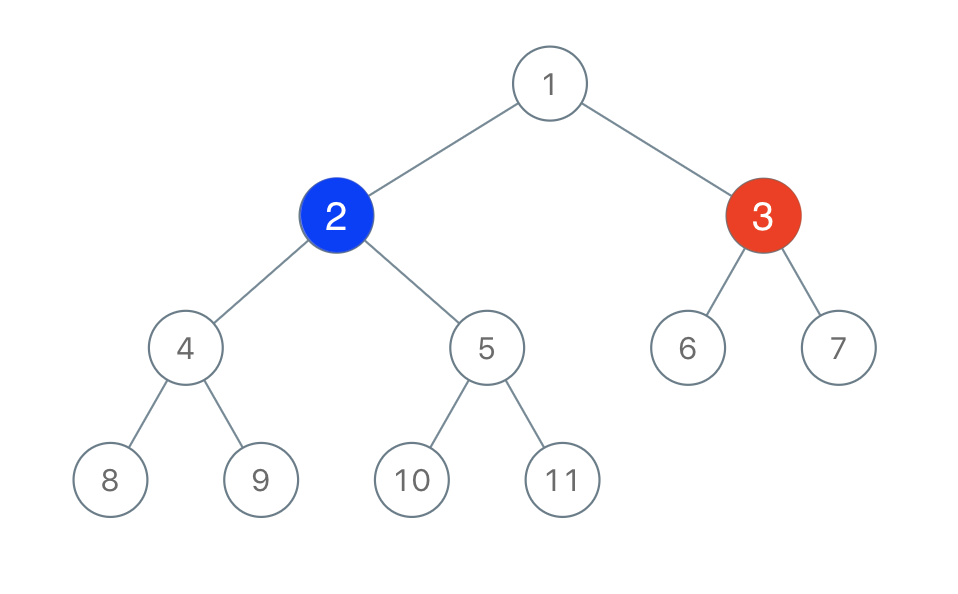
输入：root = [1,2,3,4,5,6,7,8,9,10,11], n = 11, x = 3
输出：True
解释：第二个玩家可以选择值为 2 的结点。

限制

• 二叉树的根结点为 root，树上由 n 个结点，结点上的值从 1 到 n 各不相同。
• n 为奇数。
• 1 <= x <= n <= 100

算法

(贪心，深度优先遍历) $O(n)$

1. 对于二号玩家，最多有三个备选的位置，一个是 x 的左结点，一个是右结点，或者是父结点。
2. 我们通过一次深度优先遍历，求出 x 左右子树的大小，以及除了 x 为根的子树之外的大小，就分别可以得到三个备选所代表的被蓝色染色结点个数。
3. 找到最大结点数的备选位置即可。

时间复杂度

• 每个位置仅访问一次，故时间复杂度为 $O(n)$。

空间复杂度

• 由于采用了递归，系统需要消耗 $O(h)$ 的空间复杂度，其中 $h$ 为树的最大高度。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int solve(TreeNode* rt, int n, int x, int& tot) {
        if (rt == NULL)
            return 0;

        int ls = solve(rt -> left, n, x, tot);
        int rs = solve(rt -> right, n, x, tot);

        if (rt -> val == x)
            tot = max(max(ls, rs), n - ls - rs - 1);

        return ls + rs + 1;
    }

    bool btreeGameWinningMove(TreeNode* root, int n, int x) {
        int tot = 0;
        solve(root, n, x, tot);
        return tot > n / 2;
    }
};