题目描述
给定一个大小为n≤106的数组。
有一个大小为k的滑动窗口,它从数组的最左边移动到最右边。
您只能在窗口中看到k个数字。
每次滑动窗口向右移动一个位置。
以下是一个例子:
该数组为[1 3 -1 -3 5 3 6 7],k为3。
窗口位置 最小值 最大值
[1 3 -1] -3 5 3 6 7 -1 3
1 [3 -1 -3] 5 3 6 7 -3 3
1 3 [-1 -3 5] 3 6 7 -3 5
1 3 -1 [-3 5 3] 6 7 -3 5
1 3 -1 -3 [5 3 6] 7 3 6
1 3 -1 -3 5 [3 6 7] 3 7
您的任务是确定滑动窗口位于每个位置时,窗口中的最大值和最小值。
输入格式
输入包含两行。
第一行包含两个整数n和k,分别代表数组长度和滑动窗口的长度。
第二行有n个整数,代表数组的具体数值。
同行数据之间用空格隔开。
输出格式
输出包含两个。
第一行输出,从左至右,每个位置滑动窗口中的最小值。
第二行输出,从左至右,每个位置滑动窗口中的最大值。
样例
输入样例:
8 3
1 3 -1 -3 5 3 6 7
输出样例:
-1 -3 -3 -3 3 3
3 3 5 5 6 7
算法一
题解
求最大值:建立一个单调递减队列,元素从左到右依次入队,入队之前必须从队列尾部开始删除那些比当前入队元素小或者相等的元素,直到遇到一个比当前入队元素大的元素,或者队列为空为止。若此时队列的大小超过窗口值,则从队头删除元素,直到队列大小小入窗口值为止。然后把当前元素插入队尾。
求最小值:建立一个单调递增队列,元素从左到右依次入队,入队之前必须从队列发问开始删除那些比当前入队元素大或者相等的元素,直到遇到一个比当前入队元素小的元素,或者队列为空为止。若此时队列的大小超过窗口值,则从队头删除元素,直到队列大小小入窗口值为止。然后把当前元素插入队尾。
设窗口大小为k,本题解法为建立两个单调队列,先从原数组中取前k个元素按上述要求入队,然后获取队头元素,再把下一个元素放入队中,再获取头元素,这样一直到最后一个元素为止。最后把答案从头到尾依次输出即可。
来看一下yxc老师讲解得思路图:
画的不好体谅一下 hh:
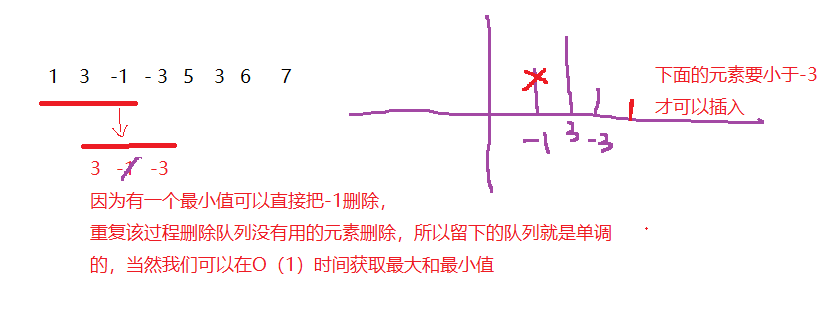
最大值的获取与最小值类似,条件不同
C++代码 (STL)
#include <iostream>
#include <cstdio>
using namespace std;
const int N = 1000005;
struct Elem
{
int val;
int pos;
};
Elem maxque[N];
Elem minque[N];
int maxhead, minhead, maxtail, mintail;
int maxans[N];
int minans[N];
int cur;
int main()
{
int n, w, num;
scanf("%d%d", &n, &w);
minhead = mintail = 0;
maxhead = maxtail = 0;
cur = 0;
for (int i = 0; i < w; ++i)
{
scanf("%d", &num);
while (minhead < mintail && minque[mintail - 1].val >= num) --mintail;
minque[mintail].val = num;
minque[mintail].pos = i;
++mintail;
while (maxhead < maxtail && maxque[maxtail - 1].val <= num) --maxtail;
maxque[maxtail].val = num;
maxque[maxtail].pos = i;
++maxtail;
}
for (int i = w; i < n; ++i)
{
minans[cur] = minque[minhead].val;
maxans[cur] = maxque[maxhead].val;
++cur;
scanf("%d", &num);
while (minhead < mintail && i - minque[minhead].pos >= w) ++minhead;
while (minhead < mintail && minque[mintail - 1].val >= num) --mintail;
minque[mintail].val = num;
minque[mintail].pos = i;
++mintail;
while (maxhead < maxtail && i - maxque[maxhead].pos >= w) ++maxhead;
while (maxhead < maxtail && maxque[maxtail - 1].val <= num) --maxtail;
maxque[maxtail].val = num;
maxque[maxtail].pos = i;
++maxtail;
}
minans[cur] = minque[minhead].val;
maxans[cur] = maxque[maxhead].val;
++cur;
for (int i = 0; i < cur; ++i)
{
if (i > 0) putchar(' ');
printf("%d", minans[i]);
}
printf("\n");
for (int i = 0; i < cur; ++i)
{
if (i > 0) putchar(' ');
printf("%d", maxans[i]);
}
printf("\n");
return 0;
}
算法2 (STL)
C++ 代码
#include <cstdio>
#include <queue>
using namespace std;
int a[1000010];
deque<int> q1,q2;
int main()
{
int n,k;
scanf("%d%d",&n,&k);
for (int i = 0;i < n; ++ i)
scanf("%d",&a[i]);
for (int i = 0;i < k ; ++ i)
{
if (q1.empty())
q1.push_back(i);
else
{
while (!q1.empty() && a[q1.back()] > a[i])
q1.pop_back();
q1.push_back(i);
}
if (q2.empty())
q2.push_back(i);
else
{
while (!q2.empty() && a[q2.back()] < a[i])
q2.pop_back();
q2.push_back(i);
}
}
printf("%d",a[q1.front()]);
for (int i = k;i < n; ++ i)
{
if (q1.front() < i - k + 1)
q1.pop_front();
while (!q1.empty() && a[q1.back()] > a[i])
q1.pop_back();
q1.push_back(i);
printf(" %d",a[q1.front()]);
}
printf("\n");
printf("%d",a[q2.front()]);
for (int i = k;i < n; ++ i)
{
if (q2.front() < i - k + 1)
q2.pop_front();
while (!q2.empty() && a[q2.back()] < a[i])
q2.pop_back();
q2.push_back(i);
printf(" %d",a[q2.front()]);
}
printf("\n");
return 0;
}
算法3 (模拟) (课上AC代码)
C++ 代码
#include<iostream>
using namespace std;
const int N=1000010;
int a[N],q[N];
int k,n;
int main(){
cin.tie(0);
ios::sync_with_stdio(false);
cin>>n>>k;
for(int i=0;i<n;i++)cin>>a[i];
int hh=0,tt=-1;
for(int i=0;i<n;i++){
if(hh<=tt&& i-k+1>q[hh])hh++;
while(hh<=tt&&a[q[tt]]>=a[i])tt--;
q[++tt]=i;
if(i>=k-1)cout<<a[q[hh]]<<" ";
}
cout<<endl;
hh=0,tt=-1;
for(int i=0;i<n;i++){
if(hh<=tt&& i-k+1>q[hh])hh++;
while(hh<=tt&&a[q[tt]]<=a[i])tt--;
q[++tt]=i;
if(i>=k-1)cout<<a[q[hh]]<<" ";
}
cout<<endl;
return 0;
}

