懒癌晚期的我把很久之前写得题解直接Copy上来qwq
这篇题解主要是写我作为一个蒟蒻的思路，dalao求轻喷qwq

思路

一般来说，做这种比较没有头绪的题一般可以先写一遍暴力，然后再寻找一下规律。

暴力

思路很容易想到：
枚举每一个点，找出它的最大流量。

那么这个最大流量怎么求呢？

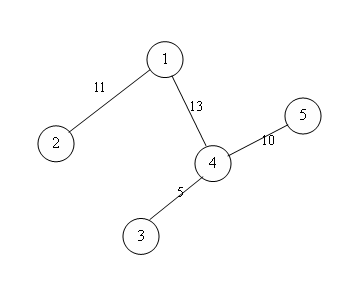
比如找$A(1)$，那么他流$13$的量到$4$，但是到出水口的水只有$10$的量，所以$1->4$这边最大量为$10$。
那么，我们可以用$dfs$回溯来完成这个过程，取叶子结点能流的最大量与父节点的最小值即可。
一旦我们搜索到出海口，直接返回它邻边的值即可。
特别注意，边界条件要放在最后。不然如果找出海口的流量就会直接返回

int dfs(int x,int l){//x为点、l为上一个点
    int p=0;//p表示叶子结点能流向海里的最大量
    for(int j=head[x];j;j=e[j].next){//它的连边
        int v=e[j].to;
        if(v==l)continue;//防止死循环
        p+=min(e[j].dis,dfs(v,x));//这个边的量
    }
    if(du[x]!=1)return d[x]=p;//du为每个点的度
    else return e[head[x]].dis;
}

但是显而易见，数据范围给的是$(N<=200000)$，如果这么做的时间复杂度为$O(N^2)$,一定会$TLE$。
所以，我们必须把时间复杂度控制在可控范围内。

想法

我们发现对于每一条边$(u, v)$，它们的最大流量似乎有迹可循，我们尝试树形$dp$换根法，观察它们之间的关系解决问题。

于是，我们思考一下，能否通过跑一遍dfs来推出其他A(x)的值？
我们注意到每次递归时有$p$的值，存在$d$数组里，思考一下是否有用？

试着跑从节点1跑一遍$dfs$，沿途把$p$用$d$数组保存起来。
$d[i]$代表$i$点下叶子结点的最大流量，当然出海口的就为$0$。

int dfs_(int x,int l){
    int p=0;d[x]=0;
    for(int j=head[x];j;j=e[j].next){
        int v=e[j].to;
        if(v==l)continue;
        p+=min(e[j].dis,dfs_(v,x));
    }
    if(du[x]!=1)return d[x]=p; 
    else return e[head[x]].dis;
}

用示例跑一遍，把$d[i]$输出：

//dp[i]代表A(i)
dp[1]=24
dp[2]=11
dp[3]=5
dp[4]=26
dp[5]=10
//d[i]代表i点下叶子结点的最大流量
d[1]=24
d[2]=0
d[3]=0
d[4]=15
d[5]=0

我们尝试着用$dp[1]$推出他相邻的点$dp[2]$，用到$dp[1]$、$d[2]$。
$dp[2]$由它的叶子结点的流量、父节点连出海口的量组成。
叶子结点，显而易见是：

d[2]

那么父节点后面的水量呢？
首先，**因为点1到点2只能流过不超过边权$(1,2)$的量。
所以：点$1$的叶子结点的最大量为：

min(边权(1,2),d[2])。
那么点1的父节点的量就是：dp[1]-min(边权(1,2),d[2]。

如果延伸到$2$，因为他们俩相连，$2$要先到$1$，才能通过$1$到$1$后面的出海口，所以水量不能超过他们俩的边权。

得推导公式：

min(边权(1,2),dp[1]-min(边权(1,2),d[2])

归纳:
任意相连的点$(u,v)$、已知$dp[u]、d[v]、边权(u,v)，$求出$dp[v]$。

dp[v]=d[v]+min(边权(u,v),dp[u]-min(边权(u,v),d[v]));

但是，还是有漏洞的，如果一开始跑$dfs$的是出海口，那么这个式子就会炸掉，$dp[u]$为0，他再减一个数字就变成负数了…这种问题很好解决，我们特判一下就行啦：

if(du[x]==1)dp[v]=e[j].dis+d[v];
else dp[v]=d[v]+min(e[j].dis,dp[x]-min(e[j].dis,d[v]));

最终，我们的推导dfs也很容易写出来啦：

void dfs(int x,int l){////x为点、l为上一个点
    for(int j=head[x];j;j=e[j].next){//找相邻点
        int v=e[j].to;
        if(v==l)continue;//防死循环
        if(du[x]==1)dp[v]=e[j].dis+d[v];
        else dp[v]=d[v]+min(e[j].dis,dp[x]-min(e[j].dis,d[v]));
        ans=max(ans,dp[v]);//找出最大的A[i]
        dfs(v,x);//继续推导
    }
}

总结

所以，我们只需要跑两遍$dfs$，第一遍算出每个点的叶子结点连得最大量$d[i]、A[1]$。再通过第二遍$dfs$逐步推出每一个$A[i]$即可。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <cmath>
using namespace std;
const int N=200001;
int t,n,u,v,w,head[N],numE=0,d[N],du[N],dp[N],ans,s;
struct Edge{
    int next,to,dis;
}e[2*N];
void addEdge(int from,int to,int dis){
    e[++numE].next=head[from];
    e[numE].to=to;
    e[numE].dis=dis;
    head[from]=numE;
}
int dfs_(int x,int l){
    int p=0;d[x]=0;
    for(int j=head[x];j;j=e[j].next){
        int v=e[j].to;
        if(v==l)continue;
        p+=min(e[j].dis,dfs_(v,x));
    }
    if(du[x]!=1)return d[x]=p; 
    else return e[head[x]].dis;
}
void dfs(int x,int l){
    for(int j=head[x];j;j=e[j].next){
        int v=e[j].to;
        if(v==l)continue;
        if(du[x]==1)dp[v]=e[j].dis+d[v];
        else dp[v]=d[v]+min(e[j].dis,dp[x]-min(e[j].dis,d[v]));
        ans=max(ans,dp[v]);
        dfs(v,x);
    }
}
int main() {
    scanf("%d",&t);
    while(t--){
        memset(head,0,sizeof(head));
        memset(d,0,sizeof(d));
        memset(dp,0,sizeof(dp));
        memset(du,0,sizeof(du));
        numE=0;ans=0;
        scanf("%d",&n);
        for(int i=1;i<n;i++){
            scanf("%d%d%d",&u,&v,&w);
            addEdge(u,v,w);addEdge(v,u,w);
            du[u]++;du[v]++;
        }
        dp[1]=dfs_(1,-1);
        dfs(1,-1);
        printf("%d\n",max(dp[1],ans));
    }
    return 0;
}