题目描述

维护一个字符串集合，支持两种操作：

“I x”向集合中插入一个字符串x；
“Q x”询问一个字符串在集合中出现了多少次。
共有N个操作，输入的字符串总长度不超过 105，字符串仅包含小写英文字母。

输入格式
第一行包含整数N，表示操作数。

接下来N行，每行包含一个操作指令，指令为”I x”或”Q x”中的一种。

输出格式
对于每个询问指令”Q x”，都要输出一个整数作为结果，表示x在集合中出现的次数。

每个结果占一行。

数据范围
1≤N≤2∗104

样例

输入样例：
5
I abc
Q abc
Q ab
I ab
Q ab
输出样例：
1
0
1

算法

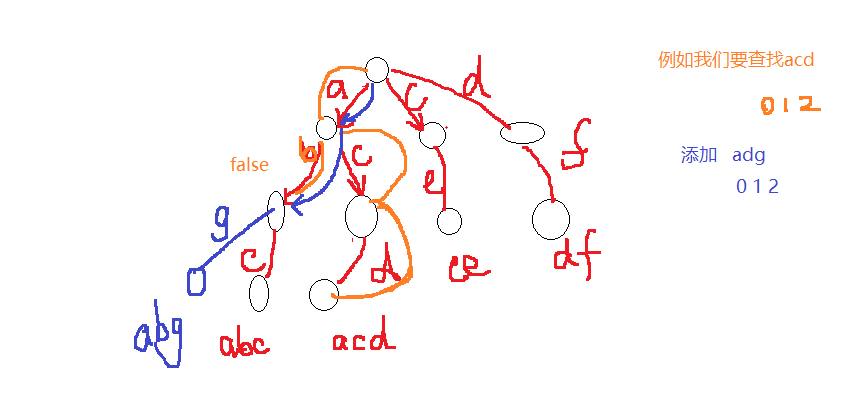
题解

1、插入过程
对于一个单词，从根开始，沿着单词的各个字母所对应的树中的节点分支向下走，直到单词遍历完，将最后的节点标记为红色，表示该单词已插入Trie树。
2、查询过程
同样的，从根开始按照单词的字母顺序向下遍历trie树，一旦发现某个节点标记不存在或者单词遍历完成而最后的节点未标记为红色，则表示该单词不存在，若最后的节点标记为红色，表示该单词存在。

模板

参数含义：

int son[N][26]; // 其中存放的是：儿子节点对应的idx。其中son数组的第一是：父节点对应的idx，第二个数是：其直接子节点('str[i]' - 'a')的值为二维下标。
int cnt [N];    // 以“abc”字符串为例，最后一个字符‘c’对应的idx作为cnt数组的下标。数组的值是该idx对应的个数。
int idx;        // 将该字符串分配的一个树结构中，以下标来记录每一个字符的位置。方便之后的插入和查找。

void insert(char str[])
{
    int p=0;
    for(int i=0;str[i];i++)   //开始下标循环
    {
        int u=str[i]-'a';   //转化值
        if(!son[p][u])son[p][u]=++idx;//  如果没有就添加
        p=son[p][u];  //有就继续检索
    }
    cnt[p]++;//单词最会一个下标值存储

}
int query(char str[]){
    int p=0;
    for(int i=0;str[i];i++){
        int u=str[i]-'a';
        if(!son[p][u])return 0;//没有就返回一
        p=son[p][u];//  有就继续检索
    }
    return cnt[p];//返回cnt的长度
}

C++ 静态代码 o(n)

include<iostream>

using namespace std;

const int N=200010;
int son[N][26],cnt[N],idx;
char str[N];
bool st[N];

int n;

void insert(char str[])
{
    int p=0;
    for(int i=0;str[i];i++){
        int u=str[i]-'a';
        if(!son[p][u])son[p][u]=++idx;
        p=son[p][u];
    }
    cnt[p]++;
}
int query(char str[]){
    int p=0;
    for(int i=0;str[i];i++){
        int u=str[i]-'a';
        if(!son[p][u])return 0;
        p=son[p][u];
    }
    return cnt[p];
}
int main(){
    cin>>n;
    while(n--){
        string op;
        cin>>op>>str;
        if(op=="I")insert(str);
        else 
        cout<<query(str)<<endl;

    }
    return 0;
}