只是打个卡,不是题解

题目描述

定义Definition:
若无向图 $G=(V,E)$ 的顶点集 $V$ 可以分割为两个互不相交的子集，且图中每条边的两个顶点分别属于不同的子集，则称图 $G$ 为一个【$\underline{\textbf{二分图}}$】

样例

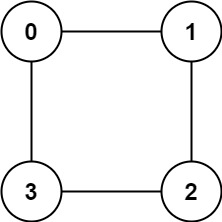
graph = [[1,3],[0,2],[1,3],[0,2]]
true

算法1

(DFS) $O()$

C++ 代码

class Solution {
private:
    static constexpr int UNCOLORED = 0;
    static constexpr int RED = 1;
    static constexpr int GREEN = 2;
    vector<int> color;
    bool valid;

public:
    void dfs(int node, int c, const vector<vector<int>>& graph) {
        color[node] = c;
        int cNei = (c == RED ? GREEN : RED);
        for (int neighbor: graph[node]) {
            if (color[neighbor] == UNCOLORED) {
                dfs(neighbor, cNei, graph);
                if (!valid) {
                    return;
                }
            }
            else if (color[neighbor] != cNei) {
                valid = false;
                return;
            }
        }
    }

    bool isBipartite(vector<vector<int>>& graph) {
        int n = graph.size();
        valid = true;
        color.assign(n, UNCOLORED);
        for (int i = 0; i < n && valid; ++i) {
            if (color[i] == UNCOLORED) {
                dfs(i, RED, graph);
            }
        }
        return valid;
    }
};