题目描述

给你一个整数数组 nums ，其中 nums[i] 表示第 i 个袋子里球的数目。同时给你一个整数 maxOperations 。

你可以进行如下操作至多 maxOperations 次：

• 选择任意一个袋子，并将袋子里的球分到 2 个新的袋子中，每个袋子里都有 正整数 个球。
  • 比方说，一个袋子里有 5 个球，你可以把它们分到两个新袋子里，分别有 1 个和 4 个球，或者分别有 2 个和 3 个球。
    你的开销是单个袋子里球数目的 最大值 ，你想要 最小化 开销。

请你返回进行上述操作后的最小开销。

样例

输入：nums = [9], maxOperations = 2
输出：3
解释：
- 将装有 9 个球的袋子分成装有 6 个和 3 个球的袋子。[9] -> [6,3] 。
- 将装有 6 个球的袋子分成装有 3 个和 3 个球的袋子。[6,3] -> [3,3,3] 。
装有最多球的袋子里装有 3 个球，所以开销为 3 并返回 3 。

输入：nums = [2,4,8,2], maxOperations = 4
输出：2
解释：
- 将装有 8 个球的袋子分成装有 4 个和 4 个球的袋子。[2,4,8,2] -> [2,4,4,4,2] 。
- 将装有 4 个球的袋子分成装有 2 个和 2 个球的袋子。[2,4,4,4,2] -> [2,2,2,4,4,2] 。
- 将装有 4 个球的袋子分成装有 2 个和 2 个球的袋子。[2,2,2,4,4,2] -> [2,2,2,2,2,4,2] 。
- 将装有 4 个球的袋子分成装有 2 个和 2 个球的袋子。[2,2,2,2,2,4,2] -> [2,2,2,2,2,2,2,2] 。
装有最多球的袋子里装有 2 个球，所以开销为 2 并返回 2 。

输入：nums = [7,17], maxOperations = 2
输出：7

提示：

1 <= nums.length <= 10^5
1 <= maxOperations, nums[i] <= 10^9

算法分析

引理(分数的上取整转换下取整)

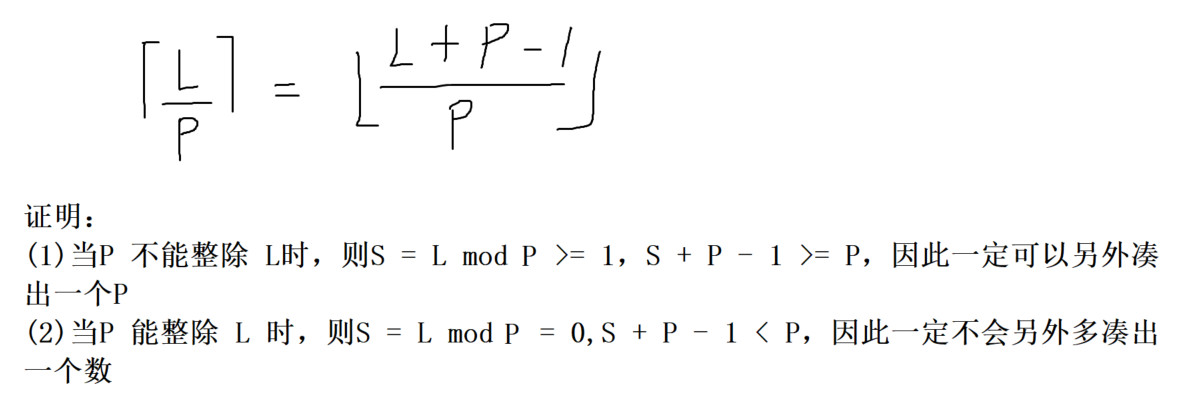
二分

• 1、对于题目意思，对于每个袋子的球，可以分到 2 个新的袋子中，每个袋子里都有 正整数 个球。题目要求求的是所有袋子中，单个袋子里球的数目的最大值的最小值
• 2、通过二分法计算出单个袋子里球的数目的最大值的最小值，若给定单个袋子的数目的最大值是x，且当前袋子的数目是k，可以将k分成$\lceil \frac{k}{x} \rceil$份，即需要操作$res = \lceil \frac{k}{x} \rceil - 1$ 份，若res <= m表示满足条件

时间复杂度 $O(nlogC)$

n是num数组的长度，C是值大小

C++ 代码

class Solution {
public:
    bool check(vector<int> &nums, int m, int x)
    {
        int res = 0;
        for(int k : nums)
        {
            res = res + (k + x - 1) / x - 1;
        }
        return res <= m;
    }
    int minimumSize(vector<int>& nums, int m) {
        //求所有袋子中，单个袋子里球的数目的最大值的最小值
        int l = 1, r = 1e9;
        while(l < r)
        {
            int mid = l + r >> 1;
            if(check(nums, m, mid)) r = mid;
            else l = mid + 1;
        }
        return l;
    }
};