题目描述

给你一个无向图，整数 n 表示图中节点的数目，edges 数组表示图中的边，其中 edges[i] = [ui, vi] ，表示 ui 和 vi 之间有一条无向边。

一个 连通三元组 指的是 三个 节点组成的集合且这三个点之间 两两 有边。

连通三元组的度数 是所有满足此条件的边的数目：一个顶点在三元组内，而另一个顶点不在三元组内。

请你返回所有连通三元组中度数的 最小值 ，如果图中没有连通三元组，那么返回 -1 。

样例

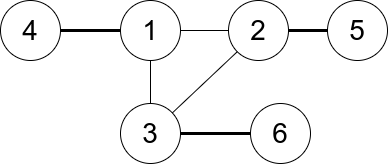
输入：n = 6, edges = [[1,2],[1,3],[3,2],[4,1],[5,2],[3,6]]
输出：3
解释：只有一个三元组 [1,2,3] 。构成度数的边在上图中已被加粗。

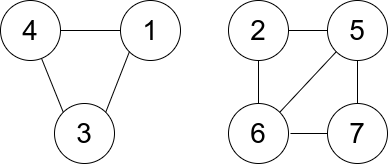
输入：n = 7, edges = [[1,3],[4,1],[4,3],[2,5],[5,6],[6,7],[7,5],[2,6]]
输出：0
解释：有 3 个三元组：
1) [1,4,3]，度数为 0 。
2) [2,5,6]，度数为 2 。
3) [5,6,7]，度数为 2 。

算法分析

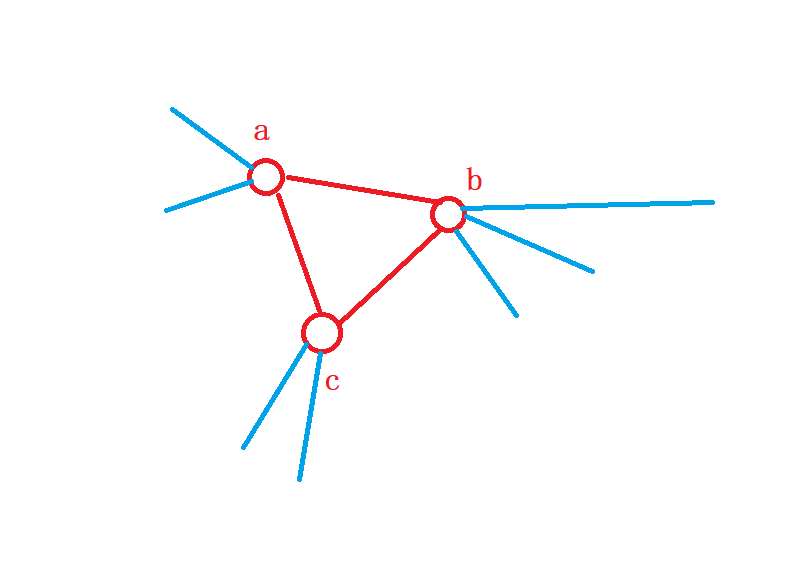
• 1、题目求的东西，找出图中的所有连通三元组，如上所示是其中一个，计算出连通三元组的最小度数，即除了内部的边以外，其他外部相连的边的总和，图中与a点相连的额外边数是2，与b点相连的额外边数是3，与c点相连的额外边数是2，因此该连通三元组的度数是2 + 3 + 2 = 7。
• 2、如何快速计算出连通三元组的度数，统计出每个点与它相连的边数，如图中所示d[a] = 4，d[b] = 5，d[c] = 4，连通三元组内部有3条边，每条边的贡献值是2，即共使用了6次，可以直接该连通三元组的度数是d[a] + d[b] + d[c] - 6
• 3、知道原理后，使用邻接矩阵建图，g[a][b] = true表示a可以到达b，统计出所有点的度数d[x]，最后3重循环枚举所有3元组，如这3个点是连通的，则调用2中的公式更新连通三元组的最小度数

时间复杂度 $O(n^3)$

C++ 代码

const int N = 410;
bool g[N][N];
int d[N];
class Solution {
public:
    int minTrioDegree(int n, vector<vector<int>>& edges) {
        memset(g, 0, sizeof g);
        memset(d, 0, sizeof d);
        for(auto& p : edges)
        {
            int a = p[0], b = p[1];
            g[a][b] = g[b][a] = true;
            d[a] ++, d[b] ++;
        }
        int res = INT_MAX;
        for(int i = 1;i <= n;i ++)
            for(int j = i + 1;j <= n;j ++)
                if(g[i][j])
                    for(int k = j + 1;k <= n;k ++)
                        if(g[i][k] && g[j][k])
                            res = min(res, d[i] + d[j] + d[k] - 6);
        if(res == INT_MAX) res = -1;
        return res;
    }
};